Some more Lagrangian Problems…

This the continuation to the first set of Lagrangian problems/solutions. While it might be a bit foolish to solve such problems, there are a few reasons why they were done:

  • Its good practice to solve some problems that are a little bit different from the norm. It’s good to be forced to think in different ways and remember some math that one may have long forgotten about from years ago.
  • Again, this is a continuation of the first set of Lagrangian based problems. That is, these problems are a stepping stone for something slightly more complicated that may or may not eventually happen.
  • The job market for solving differential equations on paper by hand and then coding them up is so tremendous. So this is good preparation if that was true. 
  • When I initially took a classical mechanics course a while ago, the professor would solve some problems to the point of having a set of differential equations. He would never proceeded onwards with those equations; the thought of using a computer and simulating them was completely foreign to him (I guess he did not know anything about computers). So simulating these simple problems is satisfying a curiosity I had a lot time ago.
  • Finally, I like classical mechanics. Sometimes I think it would be great to be stuck on an island somewhere with a pad of paper, a pen, and one of the more famous classical mechanics books out there (like this one). Other days I think it might not be the best idea.

So in this project, three more problems were solved: 1) a simple pendulum on a wheel; 2) spring-cart-pendulum system; and 3) the triple pendulum.

Simple Pendulum on a Wheel

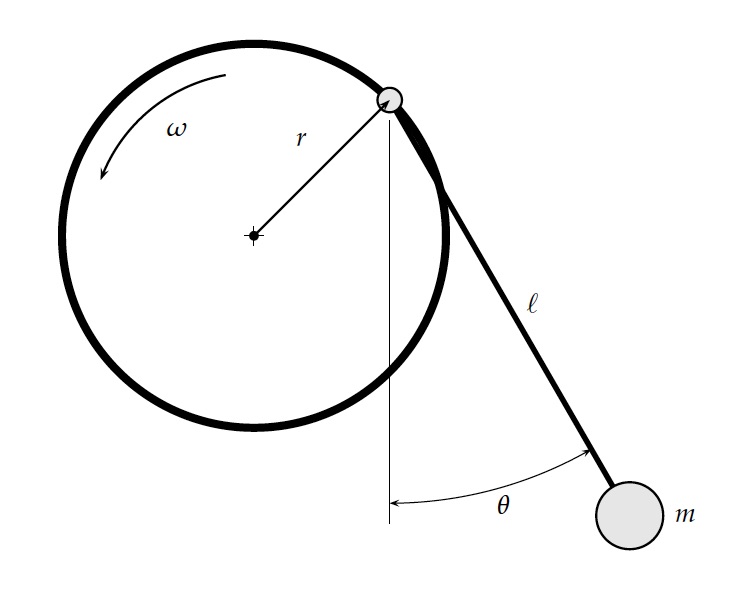
This problem is what the title says, a simple pendulum that is attached to a rotating wheel (that is rotating at a constant velocity). Note, to keep things easy, inertia is not considered in the wheels motion.

The math is pretty easy since it’s just a single degree of freedom problem. First, the angle (ϕ\phi) of where the pendulum’s pivot is on the wheel is at time t is: \phi = \phi_0 + \omega t

Where ϕ0\phi_0 is the initial angle and ω\omega is the angular speed of the rotating wheel.

The position of the pendulum’s pivot is then:x_{\mathsf{pivot}} = r \cos \omega t \qquad\qquad y_{\mathsf{pivot}} = r \sin \omega t

The pendulum’s mass position is:x_{\mathsf{pend}} = \ell \sin \theta \qquad\qquad y_{\mathsf{pend}} = -\ell \cos \theta

Therefore the final/total position of the pendulum is:

x=xpivot+xpend=rcos⁡ωt+ℓsin⁡θy=ypivot+ypend=rsin⁡ωt–ℓcos⁡θ\begin{aligned} x &= x_{\mathsf{pivot}} + x_{\mathsf{pend}} = r \cos \omega t + \ell \sin \theta \\ y &= y_{\mathsf{pivot}} + y_{\mathsf{pend}} = r \sin \omega t – \ell \cos \theta \end{aligned}

Now the velocities will be found to make the kinetic energy calculations a little bit easier to determine.

x˙=−rωsin⁡ωt+ℓcos⁡θθ˙y˙=rωcos⁡ωt+ℓsin⁡θθ˙\begin{aligned} \dot{x} &= -r\omega \sin\omega t + \ell \cos \theta \dot{\theta} \\ \dot{y} &= r\omega \cos \omega t + \ell \sin \theta \dot{\theta} \end{aligned}

Now computing the kinetic energy:

T=12mv2=12m[12x˙2+y˙2]=12m[12(−rωsin⁡ωt+ℓcos⁡θθ˙)2+(rωcos⁡ωt+ℓsin⁡θθ˙)2]=12m[12r2ω2sin⁡2ωt − 2rℓωcos⁡θsin⁡ωtθ˙ + ℓ2cos⁡2θθ˙2+r2ω2cos⁡2ωt + 2rℓωsin⁡θcos⁡ωtθ˙+ℓ2sin⁡2θθ˙212]=12mr2ω2+12mℓ2θ˙2+mrℓωsin⁡(θ–ωt)θ˙\begin{aligned} T &= \frac{1}{2} mv^2 = \frac{1}{2} m \left[ \vphantom{\frac{1}{2}} \dot{x}^2 + \dot{y}^2 \right] \\ &= \frac{1}{2} m \left[ \vphantom{\frac{1}{2}} (-r\omega \sin\omega t + \ell \cos \theta \dot{\theta})^2 + (r\omega \cos \omega t + \ell \sin \theta \dot{\theta})^2 \right] \\ &= \frac{1}{2} m \left[ \vphantom{\frac{1}{2}} r^2 \omega^2 \sin^2 \omega t \ -\ 2r\ell \omega \cos\theta\sin\omega t \dot{\theta}\ +\ \ell^2\cos^2\theta \dot{\theta}^2 \right.\\ & \qquad\quad \left. + r^2\omega^2 \cos^2\omega t\ +\ 2r\ell\omega\sin\theta\cos\omega t\dot{\theta} + \ell^2\sin^2\theta \dot{\theta}^2 \vphantom{\frac{1}{2}}\right]\\ &= \frac{1}{2} m r^2\omega^2 + \frac{1}{2} m\ell^2 \dot{\theta}^2 + mr\ell\omega \sin(\theta – \omega t)\dot{\theta} \end{aligned}

Next, the potential energy:

V=mgh=mgrsin⁡ωt–mgℓcos⁡θV = mgh = mgr \sin \omega t – mg \ell \cos \theta

So the Lagrangian becomes:

L=T − V=12mr2ω2+12mℓ2θ˙2+mrℓωsin⁡(θ–ωt)θ˙–mgrsin⁡ωt+mgℓcos⁡θ\begin{aligned} \mathcal{L} &= T\ -\ V\\ &= \frac{1}{2} m r^2\omega^2 + \frac{1}{2} m\ell^2 \dot{\theta}^2 + mr\ell\omega \sin(\theta – \omega t)\dot{\theta} – mgr \sin \omega t + mg \ell \cos \theta \end{aligned}

Now taking some derivatives so that the equation of motion can be found:

∂L∂θ˙=mℓ2θ˙ + mrℓωsin⁡(θ–ωt)ddt(∂L∂θ˙)=mℓ2θ¨ + mrℓωcos⁡(θ–ωt)⋅(θ˙–ω)=mℓ2θ¨ + mrℓωcos⁡(θ–ωt)θ˙ − mrℓω2cos⁡(θ–ωt)∂L∂θ=mrℓωcos⁡(θ–ωt)θ˙ − mgℓsin⁡θddt(∂L∂θ˙) − ∂L∂θ=mℓ2θ¨ − mrℓω2cos⁡(θ–ωt)+mgℓsin⁡θ\begin{aligned} \frac{\partial \mathcal{L}}{\partial \dot{\theta}} &= m\ell^2 \dot{\theta}\ +\ mr\ell\omega \sin (\theta – \omega t) \\ \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{\theta}} \right) &= m\ell^2 \ddot{\theta}\ +\ mr\ell\omega \cos (\theta – \omega t)\cdot(\dot{\theta} – \omega) \\ &= m\ell^2 \ddot{\theta}\ +\ mr\ell\omega \cos (\theta – \omega t)\dot{\theta}\ -\ mr\ell\omega^2 \cos (\theta – \omega t) \\ \frac{\partial \mathcal{L}}{\partial \theta} &= mr\ell\omega \cos (\theta – \omega t)\dot{\theta}\ -\ mg\ell\sin\theta \\ \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{\theta}} \right)\ -\ \frac{\partial \mathcal{L}}{\partial \theta} &= m\ell^2 \ddot{\theta}\ -\ mr\ell\omega^2 \cos(\theta – \omega t) + mg\ell\sin\theta \end{aligned}

Then after dividing everything by mℓ2m\ell^2, the final equation of motion becomes:

θ¨ − rω2ℓcos⁡(θ–ωt) + gℓsin⁡θ = 0\ddot{\theta}\ -\ \frac{r\omega^2}{\ell} \cos(\theta – \omega t)\ +\ \frac{g}{\ell}\sin \theta\ =\ 0

From the final equation of motion, there are two things to note: 1) the mass does not matter; 2) if r or ω\omega are 0, then the system reduces to a simple pendulum. Below is a small simulation of the system.

Click here to view in a separate tab.

Spring-Cart-Pendulum System

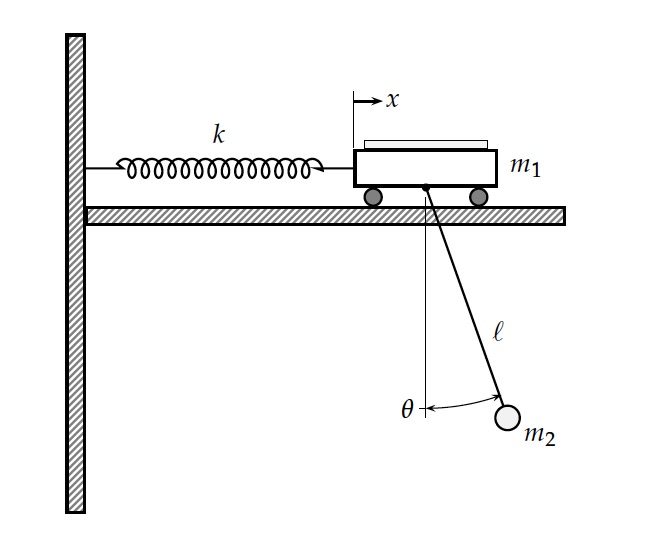
Classic problem involving a spring, pendulum, and horizontal motion. It is popular in the classroom, but I haven’t seen too many demos of it so I decided to make one here.

There are two things that are moving: the cart and the pendulum.

For the cart we have:

Cart Position=xCart Velocity=x˙\mathsf{Cart\ Position} = x \qquad\qquad \mathsf{Cart\ Velocity} = \dot{x}

For the pendulum we have:

Pendulum Position: x=ℓsin⁡θy=−ℓcos⁡θPendulum Velocity: x˙=ℓcos⁡θ⋅θ˙y˙=ℓsin⁡θ⋅θ˙\begin{aligned} \mathsf{Pendulum\ Position:}\ x &= \ell \sin \theta \\ y &= -\ell \cos \theta \\ \mathsf{Pendulum\ Velocity:}\ \dot{x} &= \ell \cos \theta \cdot \dot{\theta} \\ \dot{y} &= \ell \sin \theta \cdot \dot{\theta} \end{aligned}

Note that since the pendulum is attached to the cart it can move horizontally.  Therefore, the total pendulum xx velocity becomes:

x˙total=x˙cart+x˙pendulum=x˙+ℓcos⁡θ⋅θ˙\begin{aligned} \dot{x}_{\mathsf{total}} &= \dot{x}_{\mathsf{cart}} + \dot{x}_{\mathsf{pendulum}} \\ &= \dot{x} + \ell \cos \theta \cdot \dot{\theta} \end{aligned}

The kinetic energy is then:

T=12mv2=(12mv2)cart+(12mv2)pendulum=12m1x˙2+ 12m2[(x˙+ℓcos⁡θ⋅θ˙)2+(ℓsin⁡θ⋅θ˙)2]=12m1x˙2+12m2[x˙2+2ℓcos⁡θx˙θ˙+ℓ2cos⁡2θθ˙2+ℓ2sin⁡2θθ˙2]=12(m1+m2)x˙2 + m2ℓcos⁡θx˙θ˙ + 12m2ℓ2θ˙2\begin{aligned} T &= \frac{1}{2} mv^2 \\ &= \left(\frac{1}{2} mv^2\right)_{\mathsf{cart}} + \left(\frac{1}{2} mv^2\right)_{\mathsf{pendulum}} \\ &= \frac{1}{2} m_1 \dot{x}^2 +\ \frac{1}{2} m_2 \left[ \left( \dot{x} + \ell\cos\theta\cdot\dot{\theta} \right)^2 + \left(\ell\sin\theta\cdot\dot{\theta}\right)^2\right] \\ &= \frac{1}{2} m_1 \dot{x}^2 + \frac{1}{2} m_2 \left[ \dot{x}^2 + 2\ell\cos\theta\dot{x}\dot{\theta} + \ell^2\cos^2\theta\dot{\theta}^2 + \ell^2\sin^2\theta\dot{\theta}^2 \right] \\ &= \frac{1}{2} (m_1 + m_2) \dot{x}^2\ +\ m_2\ell\cos\theta\dot{x}\dot{\theta}\ +\ \frac{1}{2}m_2\ell^2\dot{\theta}^2 \end{aligned}

The potential energy is:

V=Vcart+Vpendulum=12k(Cart Position)2 + mg(Pendulum y Position)=12kx2 + mg(−ℓcos⁡θ)=12kx2 − m2gℓcos⁡θ\begin{aligned} V &= V_{\mathsf{cart}} + V_{\mathsf{pendulum}} \\ &= \frac{1}{2}k(\mathsf{Cart\ Position})^2\ +\ mg (\mathsf{Pendulum}\ y\ \mathsf{Position}) \\ &= \frac{1}{2}kx^2\ +\ mg (-\ell \cos \theta) \\ &= \frac{1}{2}kx^2\ -\ m_2 g \ell \cos \theta \end{aligned}

The Lagrangian becomes:

L=T − V=12(m1+m2)x˙2 + m2ℓcos⁡θx˙θ˙ + 12m2ℓ2θ˙2− 12kx2 + m2gℓcos⁡θ\begin{aligned} L &= T\ -\ V \\ &= \frac{1}{2} (m_1 + m_2) \dot{x}^2\ +\ m_2\ell\cos\theta\dot{x}\dot{\theta}\ +\ \frac{1}{2}m_2\ell^2\dot{\theta}^2 -\ \frac{1}{2}kx^2\ +\ m_2 g \ell \cos \theta \end{aligned}

Since we have two variables (x and θx\ \text{and}\ \theta), we will have two equations of motion. Solving for xx first:

∂L∂x˙=(m1+m2)x˙ + m2ℓcos⁡θθ˙ddt(∂L∂x˙)=(m1+m2)x¨ + m2ℓcos⁡θθ¨ − m2ℓsin⁡θθ˙2∂L∂x=–kxddt(∂L∂x˙) − ∂L∂x=(m1+m2)x¨ + m2ℓcos⁡θθ¨ − m2ℓsin⁡θθ˙2 + kx\begin{aligned} \frac{\partial \mathcal{L}}{\partial \dot{x}} &= (m_1 + m_2)\dot{x}\ +\ m_2\ell\cos\theta\dot{\theta} \\ \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{x}} \right) &= (m_1 + m_2)\ddot{x}\ +\ m_2\ell\cos\theta\ddot{\theta} \ -\ m_2\ell\sin\theta\dot{\theta}^2 \\ \frac{\partial \mathcal{L}}{\partial x} &= – kx \\ \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{x}} \right)\ -\ \frac{\partial \mathcal{L}}{\partial x} &= (m_1 + m_2)\ddot{x}\ +\ m_2\ell\cos\theta\ddot{\theta}\ -\ m_2\ell\sin\theta\dot{\theta}^2\ +\ kx \end{aligned}

Now dealing with θ\theta:

∂L∂θ˙=m2ℓcos⁡θx˙+m2ℓ2θ˙ddt(∂L∂θ˙)=m2ℓcos⁡θx¨–m2ℓsin⁡θx˙θ˙+m2ℓ2θ¨∂L∂θ=−m2ℓsin⁡θx˙θ˙–m2gℓsin⁡θ=–[m2ℓsin⁡θx˙θ˙+m2gℓsin⁡θ]ddt(∂L∂θ˙) − ∂L∂θ=m2ℓcos⁡θx¨ − m2ℓsin⁡θx˙θ˙ + m2ℓ2θ¨+ m2ℓsin⁡θx˙θ˙ + m2gℓsin⁡θ=m2ℓcos⁡θx¨ + m2ℓ2θ¨ + m2gℓsin⁡θ\begin{aligned} \frac{\partial \mathcal{L}}{\partial \dot{\theta}} &= m_2\ell\cos\theta\dot{x} + m_2\ell^2\dot{\theta} \\ \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{\theta}} \right) &= m_2\ell\cos\theta\ddot{x} – m_2\ell\sin\theta\dot{x}\dot{\theta} + m_2\ell^2\ddot{\theta} \\ \frac{\partial \mathcal{L}}{\partial \theta} &= -m_2\ell\sin\theta\dot{x}\dot{\theta} – m_2g\ell\sin\theta \\ &= – \left[ m_2\ell\sin\theta\dot{x}\dot{\theta} + m_2g\ell\sin\theta \right] \\ \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{\theta}} \right)\ -\ \frac{\partial \mathcal{L}}{\partial \theta} &= m_2\ell\cos\theta\ddot{x}\ -\ m_2\ell\sin\theta\dot{x}\dot{\theta}\ +\ m_2\ell^2\ddot{\theta} \\ &\qquad +\ m_2\ell\sin\theta\dot{x}\dot{\theta}\ +\ m_2g\ell\sin\theta \\ &= m_2\ell\cos\theta\ddot{x}\ +\ m_2\ell^2\ddot{\theta}\ +\ m_2g\ell\sin\theta \\ \end{aligned}

Therefore, the final equations of motion are:

(m1+m2)x¨ + m2ℓcos⁡θθ¨ − m2ℓsin⁡θθ˙2 + kx=0m2ℓcos⁡θx¨ + m2ℓ2θ¨ + m2gℓsin⁡θ=0\begin{aligned} (m_1 + m_2)\ddot{x}\ +\ m_2\ell\cos\theta\ddot{\theta}\ -\ m_2\ell\sin\theta\dot{\theta}^2\ +\ kx &= 0 \\ m_2\ell\cos\theta\ddot{x}\ +\ m_2\ell^2\ddot{\theta}\ +\ m_2g\ell\sin\theta &= 0 \end{aligned}

Solving using some matrix magic:

[m1+m2m2ℓcos⁡θm2ℓcos⁡θm2ℓ2][x¨θ¨]=[m2ℓsin⁡θθ˙2 − kx−m2gℓsin⁡θ][x¨θ¨]=[m1+m2m2ℓcos⁡θm2ℓcos⁡θm2ℓ2]−1[m2ℓsin⁡θθ˙2 − kx−m2gℓsin⁡θ]\begin{aligned} \left[ \begin{array}{cc} m_1 + m_2 & m_2\ell\cos\theta \\ m_2\ell\cos\theta & m_2\ell^2 \end{array} \right] \left[ \begin{array}{c} \ddot{x} \\ \ddot{\theta} \end{array} \right] &= \left[ \begin{array}{c} m_2\ell\sin\theta\dot{\theta}^2\ -\ kx \\ -m_2g\ell\sin\theta \end{array} \right] \\ \left[ \begin{array}{c} \ddot{x} \\ \ddot{\theta} \end{array} \right] &= \left[ \begin{array}{cc} m_1 + m_2 & m_2\ell\cos\theta \\ m_2\ell\cos\theta & m_2\ell^2 \end{array} \right]^{-1} \left[ \begin{array}{c} m_2\ell\sin\theta\dot{\theta}^2\ -\ kx \\ -m_2g\ell\sin\theta \end{array} \right] \end{aligned}

The final equations are then used when numerically solving the system. Below is a simple simulation of the using the above equations.

Click here to view in a separate tab.

Triple Pendulum

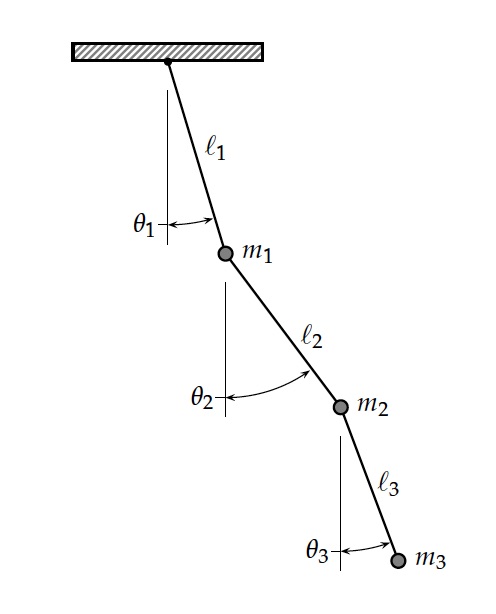
Here the triple pendulum is solved, since I have already solved the simple and double pendulum problems. Perhaps in the future, I will tackle the n-link pendulum problem (oh to dare to dream). 

The geometry of the pendulum in this video is slightly different than the one in my solution, however the video is ridiculous (I can’t believe that I search youtube for such things).

The math is not hard, just lengthy. So first looking at the positions of the masses:

x1=ℓ1sin⁡θ1y1=−ℓ1cos⁡θ1x2=ℓ1sin⁡θ1+ℓ2sin⁡θ2=x1+ℓ2sin⁡θ2y2=−ℓ1cos⁡θ1–ℓ2cos⁡θ2=y2–ℓ2cos⁡θ2x3=ℓ1sin⁡θ1+ℓ2sin⁡θ2+ℓ3sin⁡θ3=x2+ℓ3sin⁡θ3y3=−ℓ1cos⁡θ1–ℓ2cos⁡θ2–ℓ3cos⁡θ3=y2–ℓ3cos⁡θ3\begin{aligned} x_1 &= \ell_1 \sin \theta_1 \\ y_1 &= -\ell_1 \cos \theta_1 \\ x_2 &= \ell_1 \sin \theta_1 + \ell_2 \sin \theta_2 = x_1 + \ell_2 \sin \theta_2 \\ y_2 &= -\ell_1 \cos \theta_1 – \ell_2 \cos \theta_2 = y_2 – \ell_2 \cos \theta_2 \\ x_3 &= \ell_1 \sin \theta_1 + \ell_2 \sin \theta_2 + \ell_3 \sin \theta_3 = x_2 + \ell_3 \sin \theta_3 \\ y_3 &= -\ell_1 \cos \theta_1 – \ell_2 \cos \theta_2 – \ell_3 \cos \theta_3 = y_2 – \ell_3 \cos \theta_3 \end{aligned}

Note that succeeding positions can be found using the previous position; this makes writing the code a bit easier. Then the speeds of the masses can be found by taking the derivatives:

x˙1=ℓ1cos⁡θ1⋅θ˙1y˙1=ℓ1sin⁡θ1⋅θ˙1x˙2=ℓ1cos⁡θ1⋅θ˙1+ℓ2cos⁡θ2⋅θ˙2y˙2=ℓ1sin⁡θ1⋅θ˙1+ℓ2sin⁡θ2⋅θ˙2x˙3=ℓ1cos⁡θ1⋅θ˙1+ℓ2cos⁡θ2⋅θ˙2+ℓ3cos⁡θ3⋅θ˙3y˙3=ℓ1sin⁡θ1⋅θ˙1+ℓ2sin⁡θ2⋅θ˙2+ℓ3sin⁡θ3⋅θ˙3\begin{aligned} \dot{x}_1 &= \ell_1 \cos \theta_1 \cdot \dot{\theta}_1 \\ \dot{y}_1 &= \ell_1 \sin \theta_1 \cdot \dot{\theta}_1 \\ \dot{x}_2 &= \ell_1 \cos \theta_1 \cdot \dot{\theta}_1 + \ell_2 \cos \theta_2 \cdot \dot{\theta}_2 \\ \dot{y}_2 &= \ell_1 \sin \theta_1 \cdot \dot{\theta}_1 + \ell_2 \sin \theta_2 \cdot \dot{\theta}_2 \\ \dot{x}_3 &= \ell_1 \cos \theta_1 \cdot \dot{\theta}_1 + \ell_2 \cos \theta_2 \cdot \dot{\theta}_2 + \ell_3 \cos \theta_3 \cdot \dot{\theta}_3 \\ \dot{y}_3 &= \ell_1 \sin \theta_1 \cdot \dot{\theta}_1 + \ell_2 \sin \theta_2 \cdot \dot{\theta}_2 + \ell_3 \sin \theta_3 \cdot \dot{\theta}_3 \end{aligned}

Now solving for the kinetic energy:

T=12mv2=12m(x˙2+y˙2)2=12m1(x˙12+y˙12)+12m2(x˙22+y˙22)+12m3(x˙32+y˙32)=12m1[(ℓ1cos⁡θ1⋅θ˙1)2+(ℓ1sin⁡θ1⋅θ˙1)2]+12m2[(ℓ1cos⁡θ1⋅θ˙1+ℓ2cos⁡θ2⋅θ˙2)2+(ℓ1sin⁡θ1⋅θ˙1+ℓ2sin⁡θ2⋅θ˙2)2]+12m3[(ℓ1cos⁡θ1⋅θ˙1+ℓ2cos⁡θ2⋅θ˙2+ℓ3cos⁡θ3⋅θ˙3)2+(ℓ1sin⁡θ1⋅θ˙1+ℓ2sin⁡θ2⋅θ˙2+ℓ3sin⁡θ3⋅θ˙3)2]=12m1[ℓ12cos⁡2θ1⋅θ˙12+ℓ12sin⁡2θ1⋅θ˙12]+12m2[ℓ12cos⁡2θ1⋅θ˙12+2ℓ1ℓ2cos⁡θ1cos⁡θ2⋅θ˙1θ˙2+ℓ22cos⁡2θ2⋅θ˙22+ℓ12sin⁡2θ1⋅θ˙12+2ℓ1ℓ2sin⁡θ1sin⁡θ2⋅θ˙1θ˙2+ℓ22sin⁡2θ2⋅θ˙22]+12m3[ℓ12cos⁡2θ1⋅θ˙12+ℓ22cos⁡2θ2⋅θ˙22+ℓ32cos⁡2θ3⋅θ˙32+ℓ12sin⁡2θ1⋅θ˙12+ℓ22sin⁡2θ2⋅θ˙22+ℓ32sin⁡2θ3⋅θ˙32+2ℓ1ℓ2cos⁡θ1cos⁡θ2⋅θ˙1θ˙2+2ℓ1ℓ3cos⁡θ1cos⁡θ3⋅θ˙1θ˙3+2ℓ2ℓ3cos⁡θ2cos⁡θ3⋅θ˙2θ˙3+2ℓ1ℓ2sin⁡θ1sin⁡θ2⋅θ˙1θ˙2+2ℓ1ℓ3sin⁡θ1sin⁡θ3⋅θ˙1θ˙3+2ℓ2ℓ3sin⁡θ2sin⁡θ3⋅θ˙2θ˙3ℓ22]=12m1(ℓ12θ˙12)+12m2(ℓ12θ˙12+ℓ22θ˙22+2ℓ1ℓ2θ˙1θ˙2(cos⁡θ1cos⁡θ2+sin⁡θ1sin⁡θ2)ℓ22)+12m3(ℓ12θ˙12+ℓ22θ˙22+ℓ32θ˙32+2ℓ1ℓ2θ˙1θ˙2(cos⁡θ1cos⁡θ2+sin⁡θ1sin⁡θ2)+2ℓ1ℓ3θ˙1θ˙3(cos⁡θ1cos⁡θ3+sin⁡θ1sin⁡θ3)+2ℓ2ℓ3θ˙2θ˙3(cos⁡θ2cos⁡θ3+sin⁡θ2sin⁡θ3)ℓ22)=12(m1+m2+m3)ℓ12θ˙12+12(m2+m3)ℓ22θ˙22+12m3ℓ32θ˙32+(m2+m3)ℓ1ℓ2θ˙1θ˙2(cos⁡θ1cos⁡θ2+sin⁡θ1sin⁡θ2)+m3ℓ1ℓ3θ˙1θ˙3(cos⁡θ1cos⁡θ3+sin⁡θ1sin⁡θ3)+m3ℓ2ℓ3θ˙2θ˙3(cos⁡θ2cos⁡θ3+sin⁡θ2sin⁡θ3)=12(m1+m2+m3)ℓ12θ˙12+12(m2+m3)ℓ22θ˙22+12m3ℓ32θ˙32+(m2+m3)ℓ1ℓ2θ˙1θ˙2cos⁡(θ1–θ2)+m3ℓ1ℓ3θ˙1θ˙3cos⁡(θ1–θ3)+m3ℓ2ℓ3θ˙2θ˙3cos⁡(θ2–θ3)\begin{aligned} T &= \frac{1}{2} mv^2 = \frac{1}{2} m \left( \sqrt{\dot{x}^2 + \dot{y}^2 }\right)^2 \\ &= \frac{1}{2} m_1 \left( \dot{x}_1^2 + \dot{y}_1^2 \right) + \frac{1}{2} m_2 \left( \dot{x}_2^2 + \dot{y}_2^2 \right) + \frac{1}{2} m_3 \left( \dot{x}_3^2 + \dot{y}_3^2 \right) \\ &= \frac{1}{2} m_1 \left[ \left( \ell_1 \cos \theta_1 \cdot \dot{\theta}_1 \right)^2 + \left( \ell_1 \sin \theta_1 \cdot \dot{\theta}_1 \right)^2 \right] \\ & \qquad + \frac{1}{2} m_2 \left[ \left( \ell_1 \cos \theta_1 \cdot \dot{\theta}_1 + \ell_2 \cos \theta_2 \cdot \dot{\theta}_2 \right)^2 + \left( \ell_1 \sin \theta_1 \cdot \dot{\theta}_1 + \ell_2 \sin \theta_2 \cdot \dot{\theta}_2 \right)^2 \right] \\ & \qquad + \frac{1}{2} m_3 \left[ \left ( \ell_1 \cos \theta_1 \cdot \dot{\theta}_1 + \ell_2 \cos \theta_2 \cdot \dot{\theta}_2 + \ell_3 \cos \theta_3 \cdot \dot{\theta}_3 \right)^2 + \left( \ell_1 \sin \theta_1 \cdot \dot{\theta}_1 + \ell_2 \sin \theta_2 \cdot \dot{\theta}_2 + \ell_3 \sin \theta_3 \cdot \dot{\theta}_3 \right)^2 \right] \\ &= \frac{1}{2} m_1 \left[ \ell_1^2 \cos^2 \theta_1 \cdot \dot{\theta}_1^2 + \ell_1^2 \sin^2 \theta_1 \cdot \dot{\theta}_1^2 \right] \\ & \qquad + \frac{1}{2} m_2 \left[ \ell_1^2 \cos^2 \theta_1 \cdot \dot{\theta}_1^2 + 2\ell_1\ell_2 \cos \theta_1 \cos \theta_2 \cdot \dot{\theta}_1 \dot{\theta}_2 + \ell_2^2 \cos^2 \theta_2 \cdot \dot{\theta}_2^2 \right. \\ & \qquad \qquad \qquad \left. + \ell_1^2 \sin^2 \theta_1 \cdot \dot{\theta}_1^2 + 2\ell_1\ell_2 \sin \theta_1 \sin \theta_2 \cdot \dot{\theta}_1 \dot{\theta}_2 + \ell_2^2 \sin^2 \theta_2 \cdot \dot{\theta}_2^2 \right] \\ & \qquad + \frac{1}{2} m_3 \left[ \ell_1^2 \cos^2 \theta_1 \cdot \dot{\theta}_1^2 + \ell_2^2 \cos^2 \theta_2 \cdot \dot{\theta}_2^2 + \ell_3^2 \cos^2 \theta_3 \cdot \dot{\theta}_3^2 + \ell_1^2 \sin^2 \theta_1 \cdot \dot{\theta}_1^2 + \ell_2^2 \sin^2 \theta_2 \cdot \dot{\theta}_2^2 + \ell_3^2 \sin^2 \theta_3 \cdot \dot{\theta}_3^2 \right. \\ & \qquad \qquad \qquad + 2 \ell_1\ell_2 \cos\theta_1\cos \theta_2 \cdot \dot{\theta}_1 \dot{\theta}_2 + 2 \ell_1\ell_3 \cos\theta_1\cos \theta_3 \cdot \dot{\theta}_1 \dot{\theta}_3 + 2 \ell_2\ell_3 \cos\theta_2\cos \theta_3 \cdot \dot{\theta}_2 \dot{\theta}_3 \\ & \qquad \qquad \qquad \left. + 2 \ell_1\ell_2 \sin\theta_1\sin \theta_2 \cdot \dot{\theta}_1 \dot{\theta}_2 + 2 \ell_1\ell_3 \sin\theta_1\sin \theta_3 \cdot \dot{\theta}_1 \dot{\theta}_3 + 2 \ell_2\ell_3 \sin\theta_2\sin \theta_3 \cdot \dot{\theta}_2 \dot{\theta}_3 \vphantom{\ell_2^2} \right] \\ &= \frac{1}{2} m_1 \left( \ell_1^2 \dot{\theta}_1^2 \right) \\ & \qquad + \frac{1}{2} m_2 \left( \ell_1^2 \dot{\theta}_1^2 + \ell_2^2\dot{\theta}_2^2 \right. \\ & \qquad \qquad \qquad \left. + 2\ell_1\ell_2\dot{\theta}_1\dot{\theta}_2\left(\cos\theta_1\cos \theta_2 + \sin\theta_1\sin \theta_2\right) \vphantom{\ell_2^2} \right) \\ & \qquad + \frac{1}{2} m_3 \left( \ell_1^2 \dot{\theta}_1^2 + \ell_2^2 \dot{\theta}_2^2 + \ell_3^2 \dot{\theta}_3^2 \right. \\ & \qquad \qquad \qquad + 2\ell_1\ell_2\dot{\theta}_1\dot{\theta}_2\left(\cos\theta_1\cos \theta_2 + \sin\theta_1\sin \theta_2\right) \\ & \qquad \qquad \qquad + 2\ell_1\ell_3\dot{\theta}_1\dot{\theta}_3\left(\cos\theta_1\cos \theta_3 + \sin\theta_1\sin \theta_3\right) \\ & \qquad \qquad \qquad \left. + 2\ell_2\ell_3\dot{\theta}_2\dot{\theta}_3\left(\cos\theta_2\cos \theta_3 + \sin\theta_2\sin \theta_3\right) \vphantom{\ell_2^2} \right) \\ &= \frac{1}{2} \left( m_1 + m_2 + m_3 \right) \ell_1^2 \dot{\theta}_1^2 + \frac{1}{2} \left( m_2 + m_3 \right) \ell_2^2 \dot{\theta}_2^2 + \frac{1}{2} m_3 \ell_3^2 \dot{\theta}_3^2 \\ & \qquad + \left( m_2 + m_3 \right) \ell_1\ell_2\dot{\theta}_1\dot{\theta}_2\left(\cos\theta_1\cos \theta_2 + \sin\theta_1\sin \theta_2\right) \\ & \qquad + m_3 \ell_1\ell_3\dot{\theta}_1\dot{\theta}_3\left(\cos\theta_1\cos \theta_3 + \sin\theta_1\sin \theta_3\right) + m_3 \ell_2\ell_3\dot{\theta}_2\dot{\theta}_3\left(\cos\theta_2\cos \theta_3 + \sin\theta_2\sin \theta_3\right) \\ &= \frac{1}{2} \left( m_1 + m_2 + m_3 \right) \ell_1^2 \dot{\theta}_1^2 + \frac{1}{2} \left( m_2 + m_3 \right) \ell_2^2 \dot{\theta}_2^2 + \frac{1}{2} m_3 \ell_3^2 \dot{\theta}_3^2 \\ & \qquad + \left( m_2 + m_3 \right) \ell_1\ell_2\dot{\theta}_1\dot{\theta}_2 \cos (\theta_1 – \theta_2) + m_3 \ell_1\ell_3\dot{\theta}_1\dot{\theta}_3 \cos(\theta_1 – \theta_3) + m_3 \ell_2\ell_3\dot{\theta}_2\dot{\theta}_3 \cos(\theta_2 – \theta_3) \\ \end{aligned}

The potential energy is:

V=mgh=m1gy1+m2gy2+m3gy3=m1g(−ℓ1cos⁡θ1)+m2g(−ℓ1cos⁡θ1–ℓ2cos⁡θ2)+m3g(−ℓ1cos⁡θ1–ℓ2cos⁡θ2–ℓ3cos⁡θ3)=−1[11(m1+m2+m3)gℓ1cos⁡θ1+(m2+m3)gℓ2cos⁡θ2+m3gℓ3cos⁡θ3]\begin{aligned} V = mgh &= m_1 g y_1 + m_2 g y_2 + m_3 g y_3 \\ &= m_1 g \left( -\ell_1 \cos \theta_1 \right) + m_2 g \left( -\ell_1 \cos \theta_1 – \ell_2 \cos \theta_2 \right) + m_3 g \left( -\ell_1 \cos \theta_1 – \ell_2 \cos \theta_2 – \ell_3 \cos \theta_3 \right) \\ &= -1 \left[ \vphantom{\frac{1}{1}} (m_1 + m_2 + m_3)g \ell_1 \cos \theta_1 + (m_2 + m_3) g \ell_2 \cos \theta_2 + m_3 g \ell_3 \cos \theta_3 \right] \\ \end{aligned}

Now computing the Lagrangian:

L=T–V=[12(m1+m2+m3)ℓ12θ˙12+12(m2+m3)ℓ22θ˙22+12m3ℓ32θ˙32+(m2+m3)ℓ1ℓ2θ˙1θ˙2cos⁡(θ1–θ2)+m3ℓ1ℓ3θ˙1θ˙3cos⁡(θ1–θ3)+m3ℓ2ℓ3θ˙2θ˙3cos⁡(θ2–θ3)11]–(−1)[11(m1+m2+m3)gℓ1cos⁡θ1+(m2+m3)gℓ2cos⁡θ2+m3gℓ3cos⁡θ3]=12(m1+m2+m3)ℓ12θ˙12+12(m2+m3)ℓ22θ˙22+12m3ℓ32θ˙32+(m2+m3)ℓ1ℓ2θ˙1θ˙2cos⁡(θ1–θ2)+m3ℓ1ℓ3θ˙1θ˙3cos⁡(θ1–θ3)+m3ℓ2ℓ3θ˙2θ˙3cos⁡(θ2–θ3)+(m1+m2+m3)gℓ1cos⁡θ1+(m2+m3)gℓ2cos⁡θ2+m3gℓ3cos⁡θ3\begin{aligned} \mathcal{L} &= T – V \\ &= \left[ \frac{1}{2} \left( m_1 + m_2 + m_3 \right) \ell_1^2 \dot{\theta}_1^2 + \frac{1}{2} \left( m_2 + m_3 \right) \ell_2^2 \dot{\theta}_2^2 + \frac{1}{2} m_3 \ell_3^2 \dot{\theta}_3^2 \right. \\ & \qquad \left. + \left( m_2 + m_3 \right) \ell_1\ell_2\dot{\theta}_1\dot{\theta}_2 \cos (\theta_1 – \theta_2) + m_3 \ell_1\ell_3\dot{\theta}_1\dot{\theta}_3 \cos(\theta_1 – \theta_3) + m_3 \ell_2\ell_3\dot{\theta}_2\dot{\theta}_3 \cos(\theta_2 – \theta_3) \vphantom{\frac{1}{1}} \right] \\ & \qquad – (-1) \left[ \vphantom{\frac{1}{1}} (m_1 + m_2 + m_3)g \ell_1 \cos \theta_1 + (m_2 + m_3) g \ell_2 \cos \theta_2 + m_3 g \ell_3 \cos \theta_3 \right] \\ &= \frac{1}{2} \left( m_1 + m_2 + m_3 \right) \ell_1^2 \dot{\theta}_1^2 + \frac{1}{2} \left( m_2 + m_3 \right) \ell_2^2 \dot{\theta}_2^2 + \frac{1}{2} m_3 \ell_3^2 \dot{\theta}_3^2 \\ & \qquad + \left( m_2 + m_3 \right) \ell_1\ell_2\dot{\theta}_1\dot{\theta}_2 \cos (\theta_1 – \theta_2) + m_3 \ell_1\ell_3\dot{\theta}_1\dot{\theta}_3 \cos(\theta_1 – \theta_3) + m_3 \ell_2\ell_3\dot{\theta}_2\dot{\theta}_3 \cos(\theta_2 – \theta_3) \\ & \qquad + (m_1 + m_2 + m_3)g \ell_1 \cos \theta_1 + (m_2 + m_3) g \ell_2 \cos \theta_2 + m_3 g \ell_3 \cos \theta_3 \\ \end{aligned}

There are a three degrees of freedom, that is θ1,θ2, and θ3\theta_1, \theta_2,\ \text{and}\ \theta_3.  So to determine the equations of motions, we need to compute:

ddt(∂L∂θ˙1)–∂L∂θ1=0ddt(∂L∂θ˙2)–∂L∂θ2=0ddt(∂L∂θ˙3)–∂L∂θ3=0\frac{d}{dt}\left( \frac{\partial\mathcal{L}}{\partial \dot{\theta}_1} \right) – \frac{\partial\mathcal{L}}{\partial \theta_1} = 0 \quad\quad \frac{d}{dt}\left( \frac{\partial\mathcal{L}}{\partial \dot{\theta}_2} \right) – \frac{\partial\mathcal{L}}{\partial \theta_2} = 0 \quad\quad \frac{d}{dt}\left( \frac{\partial\mathcal{L}}{\partial \dot{\theta}_3} \right) – \frac{\partial\mathcal{L}}{\partial \theta_3} = 0

Solving for θ1\theta_1:

∂L∂θ˙1=(m1+m2+m3)ℓ12θ˙1+(m2+m3)ℓ1ℓ2cos⁡(θ1–θ2)θ˙2+m3ℓ1ℓ3cos⁡(θ1–θ3)θ˙3ddt(∂L∂θ˙1)=(m1+m2+m3)ℓ12θ¨1+(m2+m3)ℓ1ℓ2cos⁡(θ1–θ2)θ¨2–(m2+m3)ℓ1ℓ2sin⁡(θ1–θ2)θ˙2(θ˙1–θ˙2)+m3ℓ1ℓ3cos⁡(θ1–θ3)θ¨3–m3ℓ1ℓ3sin⁡(θ1–θ3)θ˙3(θ˙1–θ˙3)=(m1+m2+m3)ℓ12θ¨1+(m2+m3)ℓ1ℓ2cos⁡(θ1–θ2)θ¨2+m3ℓ1ℓ3cos⁡(θ1–θ3)θ¨3–(m2+m3)ℓ1ℓ2sin⁡(θ1–θ2)θ˙1θ˙2+(m1+m3)ℓ1ℓ2sin⁡(θ1–θ2)θ˙22–m3ℓ1ℓ3sin⁡(θ1–θ3)θ˙1θ˙3+m3ℓ1ℓ3sin⁡(θ1–θ3)θ˙32∂L∂θ1=–(m2+m3)ℓ1ℓ2sin⁡(θ1–θ2)θ˙1θ˙2–m3ℓ1ℓ3sin⁡(θ1–θ3)θ˙1θ˙3–(m1+m2+m3)gℓ1sin⁡θ1=−1[12(m2+m3)ℓ1ℓ2sin⁡(θ1–θ2)θ˙1θ˙2+m3ℓ1ℓ3sin⁡(θ1–θ3)θ˙1θ˙3+(m1+m2+m3)gℓ1sin⁡θ1]ddt(∂L∂θ˙1)–∂L∂θ1=(m1+m2+m3)ℓ12θ¨1+(m2+m3)ℓ1ℓ2cos⁡(θ1–θ2)θ¨2+m3ℓ1ℓ3cos⁡(θ1–θ3)θ¨3–(m1+m3)ℓ1ℓ2sin⁡(θ1–θ2)θ˙1θ˙2+(m2+m3)ℓ1ℓ2sin⁡(θ1–θ2)θ˙22–m3ℓ1ℓ3sin⁡(θ1–θ3)θ˙1θ˙3+m3ℓ1ℓ3sin⁡(θ1–θ3)θ˙32–(−1)[12(m2+m3)ℓ1ℓ2sin⁡(θ1–θ2)θ˙1θ˙2+m3ℓ1ℓ3sin⁡(θ1–θ3)θ˙1θ˙3+(m1+m2+m3)gℓ1sin⁡θ1]=(m1+m2+m3)ℓ12θ¨1+(m2+m3)ℓ1ℓ2cos⁡(θ1–θ2)θ¨2+m3ℓ1ℓ3cos⁡(θ1–θ3)θ¨3+(m2+m3)ℓ1ℓ2sin⁡(θ1–θ2)θ˙22+m3ℓ1ℓ3sin⁡(θ1–θ3)θ˙32+(m1+m2+m3)gℓ1sin⁡θ1\begin{aligned} \frac{\partial \mathcal{L}}{\partial \dot{\theta}_1} &= (m_1 + m_2 + m_3)\ell_1^2 \dot{\theta}_1 + (m_2 + m_3)\ell_1\ell_2 \cos(\theta_1 – \theta_2)\dot{\theta}_2 + m_3 \ell_1 \ell_3 \cos (\theta_1 – \theta_3)\dot{\theta}_3 \\ \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{\theta}_1} \right) &= (m_1 + m_2 + m_3)\ell_1^2 \ddot{\theta}_1 \\ & \qquad + (m_2 + m_3)\ell_1\ell_2 \cos(\theta_1 – \theta_2)\ddot{\theta}_2 – (m_2 + m_3)\ell_1\ell_2 \sin(\theta_1 – \theta_2)\dot{\theta}_2\left(\dot{\theta}_1 – \dot{\theta}_2 \right) \\ & \qquad + m_3 \ell_1 \ell_3 \cos (\theta_1 – \theta_3)\ddot{\theta}_3 – m_3 \ell_1 \ell_3 \sin (\theta_1 – \theta_3)\dot{\theta}_3 \left( \dot{\theta}_1 – \dot{\theta}_3 \right) \\ &= (m_1 + m_2 + m_3)\ell_1^2 \ddot{\theta}_1 + (m_2 + m_3)\ell_1\ell_2 \cos(\theta_1 – \theta_2)\ddot{\theta}_2 + m_3 \ell_1 \ell_3 \cos (\theta_1 – \theta_3)\ddot{\theta}_3 \\ & \qquad – (m_2 + m_3)\ell_1\ell_2 \sin(\theta_1 – \theta_2)\dot{\theta}_1\dot{\theta}_2 + (m_1 + m_3)\ell_1\ell_2 \sin(\theta_1 – \theta_2)\dot{\theta}_2^2 \\ & \qquad – m_3 \ell_1 \ell_3 \sin (\theta_1 – \theta_3)\dot{\theta}_1\dot{\theta}_3 + m_3 \ell_1 \ell_3 \sin (\theta_1 – \theta_3)\dot{\theta}_3^2 \\ \frac{\partial \mathcal{L}}{\partial \theta_1} &= – (m_2 + m_3)\ell_1 \ell_2 \sin (\theta_1 – \theta_2) \dot{\theta}_1 \dot{\theta}_2 – m_3 \ell_1 \ell_3 \sin (\theta_1 – \theta_3) \dot{\theta}_1\dot{\theta}_3 – (m_1 + m_2 + m_3) g \ell_1 \sin \theta_1 \\ &= -1 \left[ \vphantom{\frac{1}{2}} (m_2 + m_3)\ell_1 \ell_2 \sin (\theta_1 – \theta_2) \dot{\theta}_1 \dot{\theta}_2 + m_3 \ell_1 \ell_3 \sin (\theta_1 – \theta_3) \dot{\theta}_1\dot{\theta}_3 + (m_1 + m_2 + m_3) g \ell_1 \sin \theta_1 \right] \\ \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{\theta}_1} \right) – \frac{\partial \mathcal{L}}{\partial \theta_1} &= (m_1 + m_2 + m_3)\ell_1^2 \ddot{\theta}_1 + (m_2 + m_3)\ell_1\ell_2 \cos(\theta_1 – \theta_2)\ddot{\theta}_2 + m_3 \ell_1 \ell_3 \cos (\theta_1 – \theta_3)\ddot{\theta}_3 \\ & \qquad – (m_1 + m_3)\ell_1\ell_2 \sin(\theta_1 – \theta_2)\dot{\theta}_1\dot{\theta}_2 + (m_2 + m_3)\ell_1\ell_2 \sin(\theta_1 – \theta_2)\dot{\theta}_2^2 \\ & \qquad – m_3 \ell_1 \ell_3 \sin (\theta_1 – \theta_3)\dot{\theta}_1\dot{\theta}_3 + m_3 \ell_1 \ell_3 \sin (\theta_1 – \theta_3)\dot{\theta}_3^2 \\ & \qquad – (-1) \left[ \vphantom{\frac{1}{2}} (m_2 + m_3)\ell_1 \ell_2 \sin (\theta_1 – \theta_2) \dot{\theta}_1 \dot{\theta}_2 + m_3 \ell_1 \ell_3 \sin (\theta_1 – \theta_3) \dot{\theta}_1\dot{\theta}_3 + (m_1 + m_2 + m_3) g \ell_1 \sin \theta_1 \right] \\ &= (m_1 + m_2 + m_3)\ell_1^2 \ddot{\theta}_1 + (m_2 + m_3)\ell_1\ell_2 \cos(\theta_1 – \theta_2)\ddot{\theta}_2 + m_3 \ell_1 \ell_3 \cos (\theta_1 – \theta_3)\ddot{\theta}_3 \\ & \qquad + (m_2 + m_3)\ell_1\ell_2 \sin(\theta_1 – \theta_2)\dot{\theta}_2^2 + m_3 \ell_1 \ell_3 \sin (\theta_1 – \theta_3)\dot{\theta}_3^2 + (m_1 + m_2 + m_3) g \ell_1 \sin \theta_1 \\ \end{aligned}

Now dealing with θ2\theta_2:

∂L∂θ˙2=(m2+m3)ℓ22θ˙2+(m2+m3)ℓ1ℓ2cos⁡(θ1–θ2)θ˙1+m3ℓ2ℓ3cos⁡(θ2–θ3)θ˙3ddt(∂L∂θ˙2)=(m2+m3)ℓ22θ¨2+(m2+m3)ℓ1ℓ2cos⁡(θ1–θ2)θ¨1+(m2+m3)ℓ1ℓ2(−1)sin⁡(θ1–θ2)θ˙1(θ1˙–θ2˙)+m3ℓ2ℓ3cos⁡(θ2–θ3)θ¨3+m3ℓ2ℓ3(−1)sin⁡(θ2–θ3)θ˙3(θ2˙–θ3˙)=(m2+m3)ℓ22θ¨2+(m2+m3)ℓ1ℓ2cos⁡(θ1–θ2)θ¨1+m3ℓ2ℓ3cos⁡(θ2–θ3)θ¨3–(m2+m3)ℓ1ℓ2sin⁡(θ1–θ2)θ˙12+(m2+m3)ℓ1ℓ2sin⁡(θ1–θ2)θ˙1θ2˙–m3ℓ2ℓ3sin⁡(θ2–θ3)θ˙2θ˙3+m3ℓ2ℓ3sin⁡(θ2–θ3)θ˙32∂L∂θ2=(m2+m3)ℓ1ℓ2θ˙1θ˙2(−1)sin⁡(θ1–θ2)(−1)+m3ℓ2ℓ3θ˙2θ˙3(−1)sin⁡(θ2–θ3)+(m2+m3)gℓ2(−1)sin⁡θ2=−1[12−(m2+m3)ℓ1ℓ2θ˙1θ˙2sin⁡(θ1–θ2)+m3ℓ2ℓ3θ˙2θ˙3sin⁡(θ2–θ3)+(m2+m3)gℓ2sin⁡θ2]ddt(∂L∂θ˙2)–∂L∂θ2=(m2+m3)ℓ22θ¨2+(m2+m3)ℓ1ℓ2cos⁡(θ1–θ2)θ¨1+m3ℓ2ℓ3cos⁡(θ2–θ3)θ¨3–(m2+m3)ℓ1ℓ2sin⁡(θ1–θ2)θ˙12+(m2+m3)ℓ1ℓ2sin⁡(θ1–θ2)θ˙1θ2˙–m3ℓ2ℓ3sin⁡(θ2–θ3)θ˙2θ˙3+m3ℓ2ℓ3sin⁡(θ2–θ3)θ˙32–(−1)[12−(m2+m3)ℓ1ℓ2θ˙1θ˙2sin⁡(θ1–θ2)+m3ℓ2ℓ3θ˙2θ˙3sin⁡(θ2–θ3)+(m2+m3)gℓ2sin⁡θ2]=(m2+m3)ℓ1ℓ2cos⁡(θ1–θ2)θ¨1+(m2+m3)ℓ22θ¨2+m3ℓ2ℓ3cos⁡(θ2–θ3)θ¨3–(m2+m3)ℓ1ℓ2sin⁡(θ1–θ2)θ˙12+m3ℓ2ℓ3sin⁡(θ2–θ3)θ˙32+(m2+m3)gℓ2sin⁡θ2\begin{aligned} \frac{\partial \mathcal{L}}{\partial \dot{\theta}_2} &= (m_2 + m_3) \ell_2^2 \dot{\theta}_2 + (m_2 + m_3) \ell_1 \ell_2 \cos (\theta_1 – \theta_2) \dot{\theta}_1 + m_3 \ell_2 \ell_3 \cos (\theta_2 – \theta_3) \dot{\theta}_3 \\ \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{\theta}_2} \right) &= (m_2 + m_3) \ell_2^2 \ddot{\theta}_2 \\ & \qquad + (m_2 + m_3) \ell_1 \ell_2 \cos (\theta_1 – \theta_2) \ddot{\theta}_1 + (m_2 + m_3) \ell_1 \ell_2 (-1)\sin (\theta_1 – \theta_2) \dot{\theta}_1 (\dot{\theta_1} – \dot{\theta_2}) \\ & \qquad + m_3 \ell_2 \ell_3 \cos (\theta_2 – \theta_3) \ddot{\theta}_3 + m_3 \ell_2 \ell_3 (-1)\sin (\theta_2 – \theta_3) \dot{\theta}_3 (\dot{\theta_2} – \dot{\theta_3}) \\ &= (m_2 + m_3) \ell_2^2 \ddot{\theta}_2 + (m_2 + m_3) \ell_1 \ell_2 \cos (\theta_1 – \theta_2) \ddot{\theta}_1 + m_3 \ell_2 \ell_3 \cos (\theta_2 – \theta_3) \ddot{\theta}_3 \\ & \qquad – (m_2 + m_3) \ell_1 \ell_2 \sin (\theta_1 – \theta_2) \dot{\theta}_1^2 + (m_2 + m_3) \ell_1 \ell_2 \sin (\theta_1 – \theta_2) \dot{\theta}_1\dot{\theta_2} \\ & \qquad – m_3 \ell_2 \ell_3 \sin (\theta_2 – \theta_3) \dot{\theta}_2\dot{\theta}_3 + m_3 \ell_2 \ell_3 \sin (\theta_2 – \theta_3) \dot{\theta}_3^2 \\ \frac{\partial \mathcal{L}}{\partial \theta_2} &= \left( m_2 + m_3 \right) \ell_1\ell_2\dot{\theta}_1\dot{\theta}_2(-1)\sin (\theta_1 – \theta_2)(-1) + m_3 \ell_2\ell_3\dot{\theta}_2\dot{\theta}_3 (-1)\sin(\theta_2 – \theta_3) + (m_2 + m_3) g \ell_2 (-1)\sin \theta_2 \\ &= -1 \left[ \vphantom{\frac{1}{2}} -\left( m_2 + m_3 \right) \ell_1\ell_2\dot{\theta}_1\dot{\theta}_2\sin (\theta_1 – \theta_2) + m_3 \ell_2\ell_3\dot{\theta}_2\dot{\theta}_3 \sin(\theta_2 – \theta_3) + (m_2 + m_3) g \ell_2 \sin \theta_2 \right] \\ \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{\theta}_2} \right) – \frac{\partial \mathcal{L}}{\partial \theta_2} &= (m_2 + m_3) \ell_2^2 \ddot{\theta}_2 + (m_2 + m_3) \ell_1 \ell_2 \cos (\theta_1 – \theta_2) \ddot{\theta}_1 + m_3 \ell_2 \ell_3 \cos (\theta_2 – \theta_3) \ddot{\theta}_3 \\ & \qquad – (m_2 + m_3) \ell_1 \ell_2 \sin (\theta_1 – \theta_2) \dot{\theta}_1^2 + (m_2 + m_3) \ell_1 \ell_2 \sin (\theta_1 – \theta_2) \dot{\theta}_1\dot{\theta_2} \\ & \qquad – m_3 \ell_2 \ell_3 \sin (\theta_2 – \theta_3) \dot{\theta}_2\dot{\theta}_3 + m_3 \ell_2 \ell_3 \sin (\theta_2 – \theta_3) \dot{\theta}_3^2 \\ & \qquad – (-1) \left[ \vphantom{\frac{1}{2}} -\left( m_2 + m_3 \right) \ell_1\ell_2\dot{\theta}_1\dot{\theta}_2\sin (\theta_1 – \theta_2) + m_3 \ell_2\ell_3\dot{\theta}_2\dot{\theta}_3 \sin(\theta_2 – \theta_3) + (m_2 + m_3) g \ell_2 \sin \theta_2 \right] \\ &= (m_2 + m_3) \ell_1 \ell_2 \cos (\theta_1 – \theta_2) \ddot{\theta}_1 + (m_2 + m_3) \ell_2^2 \ddot{\theta}_2 + m_3 \ell_2 \ell_3 \cos (\theta_2 – \theta_3) \ddot{\theta}_3 \\ & \qquad – (m_2 + m_3) \ell_1 \ell_2 \sin (\theta_1 – \theta_2) \dot{\theta}_1^2 + m_3 \ell_2 \ell_3 \sin (\theta_2 – \theta_3) \dot{\theta}_3^2 + (m_2 + m_3) g \ell_2 \sin \theta_2 \end{aligned}

And finally θ3\theta_3:

∂L∂θ˙3=m3ℓ32θ˙3+m3ℓ1ℓ3θ˙1cos⁡(θ1–θ3)+m3ℓ2ℓ3θ˙2cos⁡(θ2–θ3)ddt(∂L∂θ˙3)=m3ℓ32θ¨3+m3ℓ1ℓ3cos⁡(θ1–θ3)θ¨1+m3ℓ1ℓ3θ˙1(−1)sin⁡(θ1–θ3)(θ˙1–θ˙3)+m3ℓ2ℓ3cos⁡(θ2–θ3)θ¨2+m3ℓ2ℓ3θ˙2(−1)sin⁡(θ2–θ3)(θ˙2–θ˙3)=m3ℓ1ℓ3cos⁡(θ1–θ3)θ¨1+m3ℓ2ℓ3cos⁡(θ2–θ3)θ¨2+m3ℓ32θ¨3–m3ℓ1ℓ3sin⁡(θ1–θ3)θ˙12+m3ℓ1ℓ3sin⁡(θ1–θ3)θ˙1θ˙3–m3ℓ2ℓ3sin⁡(θ2–θ3)θ˙22+m3ℓ2ℓ3sin⁡(θ2–θ3)θ˙2θ˙3∂L∂θ3=m3ℓ1ℓ3θ˙1θ˙3(−1)sin⁡(θ1–θ3)(−1)+m3ℓ2ℓ3θ˙2θ˙3(−1)sin⁡(θ2–θ3)(−1)+m3gℓ3(−1)sin⁡θ3=m3ℓ1ℓ3sin⁡(θ1–θ3)θ˙1θ˙3+m3ℓ2ℓ3sin⁡(θ2–θ3)θ˙2θ˙3–m3gℓ3sin⁡θ3ddt(∂L∂θ˙3)–∂L∂θ3=m3ℓ1ℓ3cos⁡(θ1–θ3)θ¨1+m3ℓ2ℓ3cos⁡(θ2–θ3)θ¨2+m3ℓ32θ¨3–m3ℓ1ℓ3sin⁡(θ1–θ3)θ˙12+m3ℓ1ℓ3sin⁡(θ1–θ3)θ˙1θ˙3–m3ℓ2ℓ3sin⁡(θ2–θ3)θ˙22+m3ℓ2ℓ3sin⁡(θ2–θ3)θ˙2θ˙3–[12m3ℓ1ℓ3sin⁡(θ1–θ3)θ˙1θ˙3+m3ℓ2ℓ3sin⁡(θ2–θ3)θ˙2θ˙3–m3gℓ3sin⁡θ3]=m3ℓ1ℓ3cos⁡(θ1–θ3)θ¨1+m3ℓ2ℓ3cos⁡(θ2–θ3)θ¨2+m3ℓ32θ¨3–m3ℓ1ℓ3sin⁡(θ1–θ3)θ˙12–m3ℓ2ℓ3sin⁡(θ2–θ3)θ˙22+m3gℓ3sin⁡θ3\begin{aligned} \frac{\partial \mathcal{L}}{\partial \dot{\theta}_3} &= m_3 \ell_3^2 \dot{\theta}_3 + m_3 \ell_1 \ell_3 \dot{\theta}_1 \cos (\theta_1 – \theta_3) + m_3 \ell_2 \ell_3 \dot{\theta}_2 \cos (\theta_2 – \theta_3) \\ \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{\theta}_3} \right) &= m_3 \ell_3^2 \ddot{\theta}_3 \\ & \qquad + m_3 \ell_1 \ell_3 \cos (\theta_1 – \theta_3) \ddot{\theta}_1 + m_3 \ell_1 \ell_3 \dot{\theta}_1 (-1) \sin (\theta_1 – \theta_3) (\dot{\theta}_1 – \dot{\theta}_3) \\ & \qquad + m_3 \ell_2 \ell_3 \cos (\theta_2 – \theta_3) \ddot{\theta}_2 + m_3 \ell_2 \ell_3 \dot{\theta}_2 (-1) \sin (\theta_2 – \theta_3) (\dot{\theta}_2 – \dot{\theta}_3) \\ &= m_3 \ell_1 \ell_3 \cos (\theta_1 – \theta_3) \ddot{\theta}_1 + m_3 \ell_2 \ell_3 \cos (\theta_2 – \theta_3) \ddot{\theta}_2 + m_3 \ell_3^2 \ddot{\theta}_3 \\ & \qquad – m_3 \ell_1 \ell_3 \sin (\theta_1 – \theta_3) \dot{\theta}_1^2 + m_3 \ell_1 \ell_3 \sin (\theta_1 – \theta_3) \dot{\theta}_1 \dot{\theta}_3 \\ & \qquad – m_3 \ell_2 \ell_3 \sin (\theta_2 – \theta_3) \dot{\theta}_2^2 + m_3 \ell_2 \ell_3 \sin (\theta_2 – \theta_3) \dot{\theta}_2 \dot{\theta}_3 \\ \frac{\partial \mathcal{L}}{\partial \theta_3} &= m_3 \ell_1 \ell_3 \dot{\theta}_1 \dot{\theta}_3 (-1) \sin ( \theta_1 – \theta_3) (-1) + m_3 \ell_2 \ell_3 \dot{\theta}_2 \dot{\theta}_3 (-1) \sin (\theta_2 – \theta_3) (-1) + m_3 g \ell_3 (-1) \sin \theta_3 \\ &= m_3 \ell_1 \ell_3 \sin (\theta_1 – \theta_3) \dot{\theta}_1 \dot{\theta}_3 + m_3 \ell_2 \ell_3 \sin (\theta_2 – \theta_3) \dot{\theta}_2 \dot{\theta}_3 – m_3 g \ell_3 \sin \theta_3 \\ \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{\theta}_3} \right) – \frac{\partial \mathcal{L}}{\partial \theta_3} &= m_3 \ell_1 \ell_3 \cos (\theta_1 – \theta_3) \ddot{\theta}_1 + m_3 \ell_2 \ell_3 \cos (\theta_2 – \theta_3) \ddot{\theta}_2 + m_3 \ell_3^2 \ddot{\theta}_3 \\ & \qquad – m_3 \ell_1 \ell_3 \sin (\theta_1 – \theta_3) \dot{\theta}_1^2 + m_3 \ell_1 \ell_3 \sin (\theta_1 – \theta_3) \dot{\theta}_1 \dot{\theta}_3 \\ & \qquad – m_3 \ell_2 \ell_3 \sin (\theta_2 – \theta_3) \dot{\theta}_2^2 + m_3 \ell_2 \ell_3 \sin (\theta_2 – \theta_3) \dot{\theta}_2 \dot{\theta}_3 \\ & \qquad – \left[ \vphantom{\frac{1}{2}} m_3 \ell_1 \ell_3 \sin (\theta_1 – \theta_3) \dot{\theta}_1 \dot{\theta}_3 + m_3 \ell_2 \ell_3 \sin (\theta_2 – \theta_3) \dot{\theta}_2 \dot{\theta}_3 – m_3 g \ell_3 \sin \theta_3 \right] \\ &= m_3 \ell_1 \ell_3 \cos (\theta_1 – \theta_3) \ddot{\theta}_1 + m_3 \ell_2 \ell_3 \cos (\theta_2 – \theta_3) \ddot{\theta}_2 + m_3 \ell_3^2 \ddot{\theta}_3 \\ & \qquad – m_3 \ell_1 \ell_3 \sin (\theta_1 – \theta_3) \dot{\theta}_1^2 – m_3 \ell_2 \ell_3 \sin (\theta_2 – \theta_3) \dot{\theta}_2^2 \\ & \qquad + m_3 g \ell_3 \sin \theta_3 \\ \end{aligned}

Therefore, the equations of motion (or governing equations) are:

(m1+m2+m3)ℓ12θ¨1+(m2+m3)ℓ1ℓ2cos⁡(θ1–θ2)θ¨2+m3ℓ1ℓ3cos⁡(θ1–θ3)θ¨3+(m2+m3)ℓ1ℓ2sin⁡(θ1–θ2)θ˙22+m3ℓ1ℓ3sin⁡(θ1–θ3)θ˙32+(m1+m2+m3)gℓ1sin⁡θ1=0(m2+m3)ℓ1ℓ2cos⁡(θ1–θ2)θ¨1+(m2+m3)ℓ22θ¨2+m3ℓ2ℓ3cos⁡(θ2–θ3)θ¨3−(m2+m3)ℓ1ℓ2sin⁡(θ1–θ2)θ˙12+m3ℓ2ℓ3sin⁡(θ2–θ3)θ˙32+(m2+m3)gℓ2sin⁡θ2=0m3ℓ1ℓ3cos⁡(θ1–θ3)θ¨1+m3ℓ2ℓ3cos⁡(θ2–θ3)θ¨2+m3ℓ32θ¨3−m3ℓ1ℓ3sin⁡(θ1–θ3)θ˙12–m3ℓ2ℓ3sin⁡(θ2–θ3)θ˙22+m3gℓ3sin⁡θ3=0\begin{aligned} (m_1 + m_2 + m_3)\ell_1^2 \ddot{\theta}_1 &+ (m_2 + m_3)\ell_1\ell_2 \cos(\theta_1 – \theta_2)\ddot{\theta}_2 + m_3 \ell_1 \ell_3 \cos (\theta_1 – \theta_3)\ddot{\theta}_3 \\ &+ (m_2 + m_3)\ell_1\ell_2 \sin(\theta_1 – \theta_2)\dot{\theta}_2^2 + m_3 \ell_1 \ell_3 \sin (\theta_1 – \theta_3)\dot{\theta}_3^2 \\ &+ (m_1 + m_2 + m_3) g \ell_1 \sin \theta_1 = 0 \\ (m_2 + m_3) \ell_1 \ell_2 \cos (\theta_1 – \theta_2) \ddot{\theta}_1 &+ (m_2 + m_3) \ell_2^2 \ddot{\theta}_2 + m_3 \ell_2 \ell_3 \cos (\theta_2 – \theta_3) \ddot{\theta}_3 \\ &- (m_2 + m_3) \ell_1 \ell_2 \sin (\theta_1 – \theta_2) \dot{\theta}_1^2 + m_3 \ell_2 \ell_3 \sin (\theta_2 – \theta_3) \dot{\theta}_3^2 \\ &+ (m_2 + m_3) g \ell_2 \sin \theta_2 = 0 \\ m_3 \ell_1 \ell_3 \cos (\theta_1 – \theta_3) \ddot{\theta}_1 &+ m_3 \ell_2 \ell_3 \cos (\theta_2 – \theta_3) \ddot{\theta}_2 + m_3 \ell_3^2 \ddot{\theta}_3 \\ &- m_3 \ell_1 \ell_3 \sin (\theta_1 – \theta_3) \dot{\theta}_1^2 – m_3 \ell_2 \ell_3 \sin (\theta_2 – \theta_3) \dot{\theta}_2^2 \\ &+ m_3 g \ell_3 \sin \theta_3 = 0 \end{aligned}

Two quick checks, if m2,m3,ℓ1,and ℓ3m_2, m_3, \ell_1, \text{and}\ \ell_3 are all 0, then the equations should reduce to a single pendulum; and if m3and ℓ3m_3 \text{and}\ \ell_3 are 0 then the system should reduce to a double pendulum.

Check 1, if m2,m3,ℓ1,and ℓ3m_2, m_3, \ell_1, \text{and}\ \ell_3 are 0, then we only have one equation:

m1ℓ12θ¨1 + m1gℓ1sin⁡θ1=0⇒θ¨1 + gℓ1sin⁡θ1=0m_1\ell_1^2 \ddot{\theta}_1\ +\ m_1 g \ell_1 \sin\theta_1 = 0 \quad \Rightarrow \quad \ddot{\theta}_1\ +\ \frac{g}{\ell_1}\sin \theta_1 = 0

And this describes a simple pendulum.

Check 2, if m3 andℓ3m_3\ \text{and} \ell_3 are 0 then, we have two equations:

(m1+m2)ℓ12θ¨1+m2ℓ1ℓ2cos⁡(θ1–θ2)θ¨2+m2ℓ1ℓ2sin⁡(θ1–θ2)θ˙22+(m1+m2)gℓ1sin⁡θ1=0m2ℓ1ℓ2cos⁡(θ1–θ2)θ¨1+m2ℓ22θ¨2–m2ℓ1ℓ2sin⁡(θ1–θ2)θ˙12+m2gℓ2sin⁡θ2=0\begin{aligned} (m_1 + m_2)\ell_1^2 \ddot{\theta}_1 + m_2\ell_1\ell_2 \cos(\theta_1 – \theta_2)\ddot{\theta}_2 + m_2\ell_1\ell_2 \sin(\theta_1 – \theta_2)\dot{\theta}_2^2 + (m_1 + m_2)g \ell_1 \sin \theta_1 &= 0 \\ m_2 \ell_1 \ell_2 \cos (\theta_1 – \theta_2) \ddot{\theta}_1 + m_2 \ell_2^2 \ddot{\theta}_2 – m_2 \ell_1 \ell_2 \sin (\theta_1 – \theta_2) \dot{\theta}_1^2 + m_2 g \ell_2 \sin \theta_2 &= 0 \\ \end{aligned}

Divide equation 1 by ℓ1\ell_1 and equation 2 by m2 and ℓ2m_2\ \text{and}\ \ell_2 and we have the equations for a double pendulum:

(m1+m2)ℓ1θ¨1+m2ℓ2cos⁡(θ1–θ2)θ¨2+m2ℓ2sin⁡(θ1–θ2)θ˙22+(m1+m2)gsin⁡θ1=0ℓ1cos⁡(θ1–θ2)θ¨1+ℓ2θ¨2–ℓ1sin⁡(θ1–θ2)θ˙12+gsin⁡θ2=0\begin{aligned} (m_1 + m_2)\ell_1 \ddot{\theta}_1 + m_2\ell_2 \cos(\theta_1 – \theta_2)\ddot{\theta}_2 + m_2\ell_2 \sin(\theta_1 – \theta_2)\dot{\theta}_2^2 + (m_1 + m_2)g \sin \theta_1 &= 0 \\ \ell_1 \cos (\theta_1 – \theta_2) \ddot{\theta}_1 + \ell_2 \ddot{\theta}_2 – \ell_1 \sin (\theta_1 – \theta_2) \dot{\theta}_1^2 + g \sin \theta_2 &= 0 \\ \end{aligned}

Looking back at the equations of motion for the triple pendulum, a little linear algebra can be used to obtain an ‘easy’ solution.

[A][θ¨i]=[B]⇒[θ¨i]=[A]−1[B]\left[ A \right] \left[ \ddot{\theta}_i \right] = \left[ B \right] \quad \Rightarrow \quad \left[ \ddot{\theta}_i \right] = \left[ A \right]^{-1} \left[ B \right]

So arranging the solution equations into matrices we have:

[(m1+m2+m3)ℓ12(m2+m3)ℓ1ℓ2cos⁡(θ1–θ2)m3ℓ1ℓ3cos⁡(θ1–θ3)(m2+m3)ℓ1ℓ2cos⁡(θ1–θ2)(m2+m3)ℓ22m3ℓ2ℓ3cos⁡(θ2–θ3)m3ℓ1ℓ3cos⁡(θ1–θ3)m3ℓ2ℓ3cos⁡(θ2–θ3)m3ℓ32][θ¨1θ¨2θ¨3]=[−(m2+m3)ℓ1ℓ2sin⁡(θ1–θ2)θ˙22–m3ℓ1ℓ3sin⁡(θ1–θ3)θ˙32–(m1+m2+m3)gℓ1sin⁡θ1(m2+m3)ℓ1ℓ2sin⁡(θ1–θ2)θ˙12–m3ℓ2ℓ3sin⁡(θ2–θ3)θ˙32–(m2+m3)gℓ2sin⁡θ2m3ℓ1ℓ3sin⁡(θ1–θ3)θ˙12+m3ℓ2ℓ3sin⁡(θ2–θ3)θ˙22–m3gℓ3sin⁡θ3]\begin{aligned} \left[ \begin{array}{ccc} (m_1 + m_2 + m_3)\ell_1^2 & (m_2 + m_3)\ell_1\ell_2 \cos(\theta_1 – \theta_2) & m_3 \ell_1 \ell_3 \cos (\theta_1 – \theta_3) \\ (m_2 + m_3) \ell_1 \ell_2 \cos (\theta_1 – \theta_2) & (m_2 + m_3) \ell_2^2 & m_3 \ell_2 \ell_3 \cos (\theta_2 – \theta_3) \\ m_3 \ell_1 \ell_3 \cos (\theta_1 – \theta_3) & m_3 \ell_2 \ell_3 \cos (\theta_2 – \theta_3) & m_3 \ell_3^2 \end{array}\right] \left[ \begin{array}{ccc} \ddot{\theta}_1 \\ \ddot{\theta}_2 \\ \ddot{\theta}_3 \end{array}\right] = \\ \left[ \begin{array}{ccc} -(m_2 + m_3)\ell_1\ell_2 \sin(\theta_1 – \theta_2)\dot{\theta}_2^2 – m_3 \ell_1 \ell_3 \sin (\theta_1 – \theta_3)\dot{\theta}_3^2 – (m_1 + m_2 + m_3) g \ell_1 \sin \theta_1 \\ (m_2 + m_3) \ell_1 \ell_2 \sin (\theta_1 – \theta_2) \dot{\theta}_1^2 – m_3 \ell_2 \ell_3 \sin (\theta_2 – \theta_3) \dot{\theta}_3^2 – (m_2 + m_3) g \ell_2 \sin \theta_2 \\ m_3 \ell_1 \ell_3 \sin (\theta_1 – \theta_3) \dot{\theta}_1^2 + m_3 \ell_2 \ell_3 \sin (\theta_2 – \theta_3) \dot{\theta}_2^2 – m_3 g \ell_3 \sin \theta_3 \end{array}\right] \end{aligned}

So then,

[θ¨1θ¨2θ¨3]=[(m1+m2+m3)ℓ12(m2+m3)ℓ1ℓ2cos⁡(θ1–θ2)m3ℓ1ℓ3cos⁡(θ1–θ3)(m2+m3)ℓ1ℓ2cos⁡(θ1–θ2)(m2+m3)ℓ22m3ℓ2ℓ3cos⁡(θ2–θ3)m3ℓ1ℓ3cos⁡(θ1–θ3)m3ℓ2ℓ3cos⁡(θ2–θ3)m3ℓ32]−1×[−(m2+m3)ℓ1ℓ2sin⁡(θ1–θ2)θ˙22–m3ℓ1ℓ3sin⁡(θ1–θ3)θ˙32–(m1+m2+m3)gℓ1sin⁡θ1(m2+m3)ℓ1ℓ2sin⁡(θ1–θ2)θ˙12–m3ℓ2ℓ3sin⁡(θ2–θ3)θ˙32–(m2+m3)gℓ2sin⁡θ2m3ℓ1ℓ3sin⁡(θ1–θ3)θ˙12+m3ℓ2ℓ3sin⁡(θ2–θ3)θ˙22–m3gℓ3sin⁡θ3]\begin{aligned} \left[ \begin{array}{ccc} \ddot{\theta}_1 \\ \ddot{\theta}_2 \\ \ddot{\theta}_3 \end{array}\right] = \left[ \begin{array}{ccc} (m_1 + m_2 + m_3)\ell_1^2 & (m_2 + m_3)\ell_1\ell_2 \cos(\theta_1 – \theta_2) & m_3 \ell_1 \ell_3 \cos (\theta_1 – \theta_3) \\ (m_2 + m_3) \ell_1 \ell_2 \cos (\theta_1 – \theta_2) & (m_2 + m_3) \ell_2^2 & m_3 \ell_2 \ell_3 \cos (\theta_2 – \theta_3) \\ m_3 \ell_1 \ell_3 \cos (\theta_1 – \theta_3) & m_3 \ell_2 \ell_3 \cos (\theta_2 – \theta_3) & m_3 \ell_3^2 \end{array}\right]^{-1} \\ \times \left[ \begin{array}{ccc} -(m_2 + m_3)\ell_1\ell_2 \sin(\theta_1 – \theta_2)\dot{\theta}_2^2 – m_3 \ell_1 \ell_3 \sin (\theta_1 – \theta_3)\dot{\theta}_3^2 – (m_1 + m_2 + m_3) g \ell_1 \sin \theta_1 \\ (m_2 + m_3) \ell_1 \ell_2 \sin (\theta_1 – \theta_2) \dot{\theta}_1^2 – m_3 \ell_2 \ell_3 \sin (\theta_2 – \theta_3) \dot{\theta}_3^2 – (m_2 + m_3) g \ell_2 \sin \theta_2 \\ m_3 \ell_1 \ell_3 \sin (\theta_1 – \theta_3) \dot{\theta}_1^2 + m_3 \ell_2 \ell_3 \sin (\theta_2 – \theta_3) \dot{\theta}_2^2 – m_3 g \ell_3 \sin \theta_3 \end{array}\right] \end{aligned}

Finally, simulating the results…

Click here to view in a separate tab.

Code

All the code was written in Javascript and the visual components were done using the Html Canvas element and is available here. The math was originally done with just pen and paper, and the code written using vi (or more precisely vim). A Latex version of the math (with not too many errors) has also been made available.

Future

Maybe in the future more Lagrangian problems will be looked at including spherical pendulums (and the Foucault pendulum) and possibly n-link pendulums.

 

No Comments

Add your comment