This project was more of a large side project than anything else. Its main purpose was to practice making some interactive graphics using the HTML Canvas. Also, it also served to help remember some of the basics with Lagrangian mechanics.
Making this project was rather fun. Depending on the workload, more Lagrangian problems will be solved in a similar manner, however they will be a bit more advanced to make things a little more challenging for myself.
Note that this document contains all of the math. I didn’t skip any steps since I wanted to make sure that I didn’t make any mistakes since it has been a while since I did such calculations.
The Lagrange Equation
There are a lot of great textbooks and online sources that explain the Lagrangian better than I can. But basically, it is the ‘next level’ of Newton’s laws of motion. It allows one to solve much more complicated dynamics systems by looking at the energy in the system.
The Lagrangian is defined as:
\begin{aligned}
\mathsf{Lagrangian} &= \mathsf{Kinetic\ Energy} – \mathsf{Potential\ Energy} \\
\mathcal{L} &= T\ -\ V
\end{aligned}
Using the Lagrangian on a conservative system, the final equations of motion can be found by:
\frac{d}{dt}\left( \frac{\partial\mathcal{L}}{\partial \dot{q}_i} \right)\ -\
\frac{\partial\mathcal{L}}{\partial q_i} = 0
Simple Pendulum
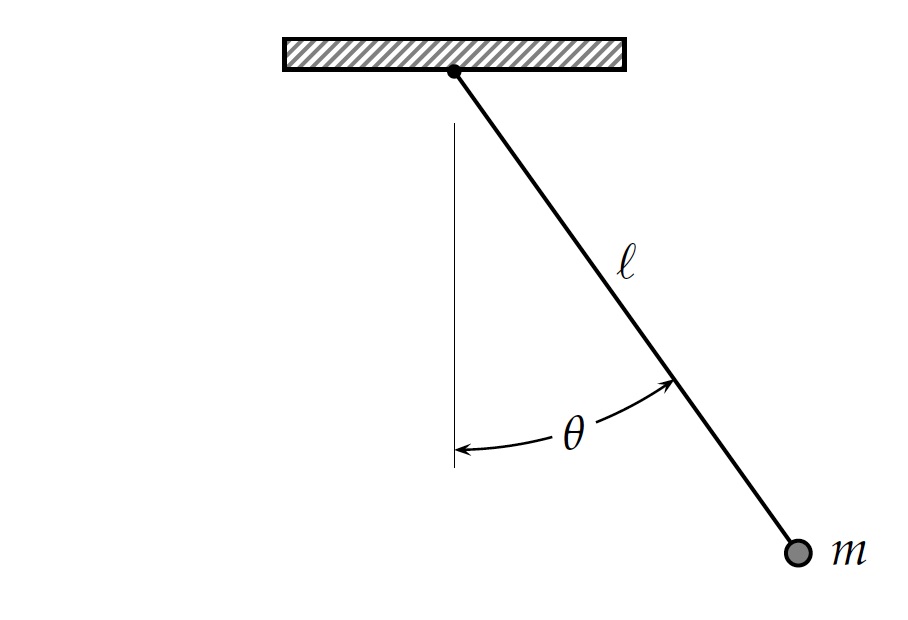
Before the solution of two more complicated systems are computed, the more simpler case, that is a simple pendulum is first examined. In such a system, a weight (usually called a bob) is attached to a string of negligible weight. The system (shown below) is a mass (m) located at the end of a string of length \ell. It only has one variable (or degree of freedom), that is the angle \theta.
If the origin is at the location of where the pendulum is fixed to the ceiling, then the location of the mass can be calculated as:
x = \ell \sin \theta \qquad\qquad
y = -\ell \cos \theta
The speed of both x and y components are:
\dot{x} = \ell \cos \theta \cdot \dot{\theta}
\qquad\qquad
\dot{y} = \ell \sin \theta \cdot \dot{\theta}
Now solving for the kinetic energy:
\begin{aligned}
T = \frac{1}{2} mv^2 &= \frac{1}{2} m \left( \sqrt{\dot{x}^2 + \dot{y}^2 }\right)^2 \\
&= \frac{1}{2} m \left( \ell^2\cos^2 \theta \cdot \dot{\theta}^2 + \ell^2\sin^2 \theta \cdot \dot{\theta}^2 \right ) \\
&= \frac{1}{2} m \ell^2\dot{\theta}^2
\end{aligned}
And the potential energy:
V = mgh = -mg \ell \cos \theta
Now the Lagrangian becomes:
\mathcal{L} = T\ -\ V = \frac{1}{2} m \ell^2\dot{\theta}^2 + mg \ell \cos \theta
Since there is only one degree of freedom, that is \theta, it’s pretty easy to solve for the equations of motion:
\begin{aligned}
\frac{\partial \mathcal{L}}{\partial \dot{\theta}} &= m\ell^2 \dot{\theta} \\
\frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{\theta}} \right) &= m\ell^2 \ddot{\theta} \\
\frac{\partial \mathcal{L}}{\partial \theta} &= -mg \ell \sin \theta
\end{aligned}
Therefore the final solution is:
\begin{aligned}
\frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{\theta}} \right)\ -\ \frac{\partial \mathcal{L}}{\partial \theta} &= 0 \\
m\ell^2 \ddot{\theta} + mg \ell \sin \theta &= 0 \\
\ddot{\theta} + \frac{g}{\ell} \sin \theta &= 0
\end{aligned}
Note that the motion does not depend on the mass.
Damped Simple Pendulum
The previous Lagrangian formula was missing any external forces, or it specifically assumed that they were zero. If any external forces are considered we get:
\frac{d}{dt}\left( \frac{\partial\mathcal{L}}{\partial \dot{q}} \right)\ -\ \frac{\partial \mathcal{L}}{\partial q} = F^\mathsf{ext} \cdot \frac{\partial r}{\partial q}
If the forces do not explicitly depend on time:
F^\mathsf{ext} \cdot \frac{\partial r}{\partial q} = – \frac{\partial F}{\partial \dot{q}}
So with any external forces we have:
\frac{d}{dt}\left( \frac{\partial\mathcal{L}}{\partial \dot{q}} \right)\ -\ \frac{\partial \mathcal{L}}{\partial q} + \frac{\partial F}{\partial \dot{q}} = 0
With a pendulum the linear damping (that is friction from rotating) can be written as:
F = \frac{1}{2}b\dot{\theta}^2
The final motion equation becomes:
\ddot{\theta} + b\dot{\theta} + \frac{g}{\ell} \sin \theta = 0
Note that the damping is just an approximation. Its main purpose is to slow down the motion so it eventually stops which will make the system appear to be slightly more realistic.
Runge Kutta Solution
In order to use the Runge Kutta technique, the solution needs to have first degree derivatives. Therefore, we need to rewrite things and use some variable substitutions to get rid of the higher order derivatives.
First we rewrite the original equation as:
\ddot{\theta} = – \frac{g}{\ell} \sin \theta\ -\ b\dot{\theta}
Then we substitute \dot{u} for \ddot{\theta} and \dot{u} for \ddot{\theta} we get:
\dot{u} = -\frac{g}{\ell} \sin \theta\ -\ bu
\qquad\qquad u = \dot{\theta}
Therefore, when using the Runge Kutta technique, the following functions are used:
\ddot{\theta} + \frac{g}{\ell} \sin \theta\ -\ b\dot{\theta}\ = 0
\qquad\Rightarrow\qquad
\left\{
\begin{array}{l}
\dot{u} = – \frac{g}{\ell} \sin \theta\ -\ bu \\
u = \dot{\theta} \\
\end{array}
\right\}
Using the above equations we are able to create the simulation of a simple pendulum with damping below (or click here to view it in a separate tab).
Double Pendulum
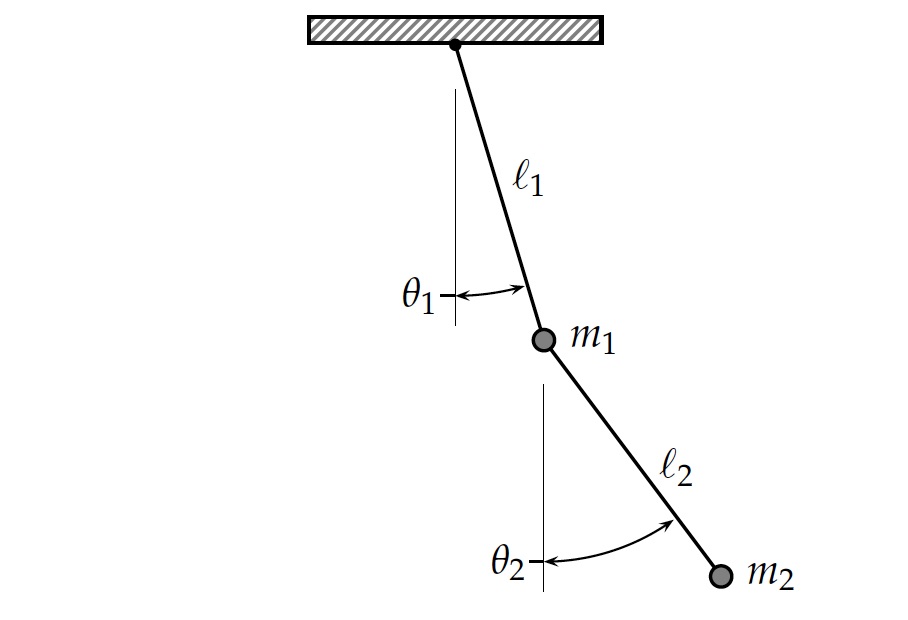
A double pendulum is perhaps one of the first problems that show the power of the Lagrangian. It is a simple pendulum attached to another simple pendulum, as shown below:
The positions of the masses can be calculated as:
\begin{aligned}
x_1 &= \ell_1 \sin \theta_1 \\
y_1 &= -\ell_1 \cos \theta_1 \\
x_2 &= \ell_1 \sin \theta_1 + \ell_2 \sin \theta_2 \\
y_2 &= -\ell_1 \cos \theta_1 – \ell_2 \cos \theta_2
\end{aligned}
The speeds of the masses are found by taking the derivatives (note to chain the angle):
\begin{aligned}
\dot{x}_1 &= \ell_1 \cos \theta_1 \cdot \dot{\theta}_1 \\
\dot{y}_1 &= \ell_1 \sin \theta_1 \cdot \dot{\theta}_1 \\
\dot{x}_2 &= \ell_1 \cos \theta_1 \cdot \dot{\theta}_1 + \ell_2 \cos \theta_2 \cdot \dot{\theta}_2 \\
\dot{y}_2 &= \ell_1 \sin \theta_1 \cdot \dot{\theta}_1 + \ell_2 \sin \theta_2 \cdot \dot{\theta}_2
\end{aligned}
Now solving for the kinetic energy:
\begin{aligned}
T = \frac{1}{2} mv^2 &= \frac{1}{2} m \left( \sqrt{\dot{x}^2 + \dot{y}^2 }\right)^2 \\
&= \frac{1}{2} m_1 \left( \dot{x}_1^2 + \dot{y}_1^2 \right) + \frac{1}{2} m_2 \left( \dot{x}_2^2 + \dot{y}_2^2 \right) \\
&= \frac{1}{2} m_1 \left( \ell_1^2 \cos^2 \theta_1 \cdot \dot{\theta}_1^2 + \ell_1^2 \sin^2 \theta_1 \cdot \dot{\theta}_1^2 \right) \\
&\qquad + \frac{1}{2} m_2 \left( \ell_1^2 \cos^2 \theta_1 \cdot \dot{\theta}_1^2 + 2 \ell_1\ell_2 \cos \theta_1 \cos \theta_2 \cdot \dot{\theta}_1\dot{\theta}_2
+ \ell_2^2 \cos^2 \theta_2^2 \cdot \dot{\theta}_2^2 \right. \\
&\qquad\qquad + \left.\ell_1^2 \sin^2 \theta_1 \cdot \dot{\theta}_1^2 + 2 \ell_1\ell_2 \sin \theta_1 \sin \theta_2 \cdot \dot{\theta}_1 \dot{\theta}_2
+ \ell_2^2 \sin^2 \theta_2 \cdot \dot{\theta}_2^2 \right) \\
&= \frac{1}{2} m_1 \ell_1^2 \dot{\theta}_1^2 + \frac{1}{2} m_2 \left( \ell_1^2 \dot{\theta}_1^2 + \ell_2^2 \dot{\theta}_2^2
+ 2 \ell_1\ell_2 \dot{\theta}_1 \dot{\theta}_2 ( \cos \theta_1 \cos \theta_2 + \sin \theta_1 \sin \theta_2 ) \right) \\
&= \frac{1}{2} m_1 \ell_1^2 \dot{\theta}_1^2 + \frac{1}{2} m_2 \ell_1^2 \dot{\theta}_1^2 + \frac{1}{2} m_2 \ell_2^2 \dot{\theta}_2^2
+ m_2 \ell_1\ell_2 \dot{\theta}_1 \dot{\theta}_2 \cos (\theta_1 – \theta_2) \\
&= \frac{1}{2} (m_1 + m_2) \ell_1^2 \dot{\theta}_1^2 + \frac{1}{2} m_2 \ell_2^2 \dot{\theta}_2^2
+ m_2 \ell_1\ell_2 \dot{\theta}_1 \dot{\theta}_2 \cos (\theta_1 – \theta_2) \\
\end{aligned}
\begin{aligned}
V = mgh &= m_1 g (-\ell_1 \cos \theta_1) + m_2 g (-\ell_1 \cos \theta_1\ -\ \ell_2 \cos \theta_2) \\
&= -m_1 g \ell_1 \cos \theta_1\ -\ m_2 g \ell_1 \cos \theta_1\ -\ m_2 g \ell_2 \cos \theta_2 \\
&= -(m_1 + m_2)g \ell_1 \cos \theta_1\ -\ m_2 g \ell_2 \cos \theta_2 \\
\end{aligned}
Combining the kinetic and potential energies to produce the the Lagrangian:
\begin{aligned}
\mathcal{L} &= T – V \\
&= \underbrace{\frac{1}{2} (m_1 + m_2) \ell_1^2 \dot{\theta}_1^2 + \frac{1}{2} m_2 \ell_2^2 \dot{\theta}_2^2
+ m_2 \ell_1\ell_2 \dot{\theta}_1 \dot{\theta}_2 \cos (\theta_1 – \theta_2)}_T \\
&\qquad + \underbrace{\vphantom{\frac{1}{2}}(m_1 + m_2)g \ell_1 \cos \theta_1 + m_2 g \ell_2 \cos \theta_2}_{-V} \\
\end{aligned}
There are a few degrees of freedom, that is \theta_1 and \theta_2. So to determine the equations of motions, we need to compute:
\frac{d}{dt}\left( \frac{\partial\mathcal{L}}{\partial \dot{\theta}_1} \right)\ -\
\frac{\partial\mathcal{L}}{\partial \theta_1} = 0
\qquad\qquad
\text{and}
\qquad\qquad
\frac{d}{dt}\left( \frac{\partial\mathcal{L}}{\partial \dot{\theta}_2} \right)\ -\
\frac{\partial\mathcal{L}}{\partial \theta_2} = 0
\begin{aligned}
\frac{\partial \mathcal{L}}{\partial \dot{\theta}_1} &= (m_1 + m_2)\ell_1^2 \dot{\theta}_1 + m_2 \ell_1 \ell_2 \cos (\theta_1 – \theta_2) \dot{\theta}_2 \\
\frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{\theta}_1} \right) &=
(m_1 + m_2)\ell_1^2 \ddot{\theta}_1 + m_2\ell_1\ell_2 \cos (\theta_1 – \theta_2) \ddot{\theta}_2\
-\ m_2\ell_1\ell_2 \dot{\theta}_2 \sin (\theta_1 – \theta_2) \cdot (\dot{\theta}_1 – \dot{\theta}_2) \\
\frac{\partial \mathcal{L}}{\partial \theta_1} &= – m_2 \ell_1\ell_2\sin (\theta_1 – \theta_2) \dot{\theta}_1 \dot{\theta}_2\ -\ (m_1 + m_2) g \ell_1 \sin \theta_1 \\
\frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{\theta}_1} \right) – \frac{\partial \mathcal{L}}{\partial \theta_1} &=
(m_1 + m_2)\ell_1^2 \ddot{\theta}_1 + m_2 \ell_1 \ell_2 \cos (\theta_1 – \theta_2) \ddot{\theta}_2\
-\ m_2\ell_1\ell_2 \dot{\theta}_2 \sin (\theta_1 – \theta_2) \cdot (\dot{\theta}_1 – \dot{\theta}_2) \\
&\qquad + m_2 \ell_1\ell_2 \sin (\theta_1 – \theta_2)\dot{\theta}_1 \dot{\theta}_2 + (m_1 + m_2) g \ell_1 \sin \theta_1 \\
&= (m_1 + m_2)\ell_1^2 \ddot{\theta}_1 + m_2 \ell_1 \ell_2 \cos (\theta_1 – \theta_2) \ddot{\theta}_2
+ m_2\ell_1\ell_2 \sin (\theta_1 – \theta_2) \dot{\theta}_2^2 + (m_1 + m_2) g \ell_1 \sin \theta_1 \\
&= (m_1 + m_2)\ell_1 \ddot{\theta}_1 + m_2 \ell_2 \cos (\theta_1 – \theta_2) \ddot{\theta}_2
+ m_2\ell_2 \sin (\theta_1 – \theta_2) \dot{\theta}_2^2 + (m_1 + m_2) g \sin \theta_1 \\
\end{aligned}
\begin{aligned}
\frac{\partial \mathcal{L}}{\partial \dot{\theta}_2} &= m_2 \ell_2^2 \dot{\theta}_2 + m_2\ell_1\ell_2 \cos(\theta_1 – \theta_2) \dot{\theta}_1 \\
\frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{\theta}_2} \right) &= m_2 \ell_2^2 \ddot{\theta}_2
+ m_2\ell_1\ell_2 \cos(\theta_1 – \theta_2) \ddot{\theta}_1\ -\ m_2\ell_1\ell_2 \sin (\theta_1 – \theta_2) \dot{\theta}_1 \cdot (\dot{\theta}_1 – \dot{\theta}_2) \\
\frac{\partial \mathcal{L}}{\partial \theta_2} &= m_2 \ell_1\ell_2 \dot{\theta}_1 \dot{\theta}_2 \sin (\theta_1 – \theta_2)\ -\ m_2 g \ell_2 \sin \theta_2 \\
\frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{\theta}_2} \right)\ -\ \frac{\partial \mathcal{L}}{\partial \theta_2} &=
m_2 \ell_2^2 \ddot{\theta}_2 + m_2\ell_1\ell_2 \cos(\theta_1 – \theta_2) \ddot{\theta}_1
-\ m_2\ell_1\ell_2 \sin (\theta_1 – \theta_2) \dot{\theta}_1 \cdot (\dot{\theta}_1 – \dot{\theta}_2) \\
&\qquad -\ m_2 \ell_1\ell_2 \dot{\theta}_1 \dot{\theta}_2 \sin (\theta_1 – \theta_2) + m_2 g \ell_2 \sin \theta_2 \\
&= m_2 \ell_2^2 \ddot{\theta}_2 + m_2\ell_1\ell_2 \cos(\theta_1 – \theta_2) \ddot{\theta}_1\ -\ m_2 \ell_1\ell_2 \sin (\theta_1 – \theta_2) \dot{\theta}_1^2
+ m_2 g \ell_2 \sin \theta_2 \\
&= \ell_2 \ddot{\theta}_2 + \ell_1 \cos(\theta_1 – \theta_2) \ddot{\theta}_1\ -\ \ell_1 \sin (\theta_1 – \theta_2) \dot{\theta}_1^2 + g \sin \theta_2 \\
\end{aligned}
Therefore, the equations of motion (or governing equations) are:
\begin{aligned}
(m_1 + m_2)\ell_1 \ddot{\theta}_1 + m_2 \ell_2 \cos (\theta_1 – \theta_2) \ddot{\theta}_2
+ m_2\ell_2 \sin (\theta_1 – \theta_2) \dot{\theta}_2^2 + (m_1 + m_2) g \sin \theta_1 &= 0 \\
\ell_2 \ddot{\theta}_2 + \ell_1 \cos(\theta_1 – \theta_2) \ddot{\theta}_1\ -\ \ell_1 \sin (\theta_1 – \theta_2) \dot{\theta}_1^2 + g \sin \theta_2 &= 0
\end{aligned}
Note that if m_2 = 0, \ell_2 = 0, and \theta_1 = \theta_2, then the equations simplify to a simple pendulum.
Solving for Runge Kutta…
In order to solve numerically, we need to clean up the math a bit. The double dot equations need to be written in terms of \theta_1, \dot{\theta_1}, \theta_2, and \dot{\theta_2}. First, we need to rearrange the equation a bit, and solve it using matrices.
\begin{aligned}
(m_1 + m_2)\ell_1 \ddot{\theta}_1 + m_2 \ell_2 \cos (\theta_1 – \theta_2) \ddot{\theta}_2 &=
– m_2\ell_2 \sin (\theta_1 – \theta_2) \dot{\theta}_2^2\ -\ (m_1 + m_2) g \sin \theta_1 \\
\ell_1 \cos(\theta_1 – \theta_2) \ddot{\theta}_1 + \ell_2 \ddot{\theta}_2 &=
\ell_1 \sin (\theta_1 – \theta_2) \dot{\theta}_1^2 – g \sin \theta_2
\end{aligned}
Rewrite the equations using some matrices:
\left[
\begin{array}{cc}
(m_1 + m_2)\ell_1 & m_2 \ell_2 \cos (\theta_1 – \theta_2) \\
\ell_1 \cos(\theta_1 – \theta_2) & \ell_2
\end{array}
\right]
\left[
\begin{array}{c}
\ddot{\theta}_1 \\
\ddot{\theta}_2
\end{array}
\right]
=
\left[
\begin{array}{c}
– m_2\ell_2 \sin (\theta_1 – \theta_2) \dot{\theta}_2^2\ -\ (m_1 + m_2) g \sin \theta_1 \\
\ell_1 \sin (\theta_1 – \theta_2) \dot{\theta}_1^2\ -\ g \sin \theta_2
\end{array}
\right]
Now the equations are in the form:
\left[
\begin{array}{cc}
m_{11} & m_{12} \\
m_{21} & m_{22}
\end{array}
\right]
\left[
\begin{array}{c}
\ddot{\theta}_1 \\
\ddot{\theta}_2
\end{array}
\right]
=
\left[
\begin{array}{c}
F_1 \\
F_2
\end{array}
\right]
So to find \ddot{\theta}_1 and \ddot{\theta}_2, we just have to just take the inverse of the M matrix and multiply by the remaining stuff on the ride hand side. That is:
\left[
\begin{array}{c}
\ddot{\theta}_1 \\
\ddot{\theta}_2
\end{array}
\right]
=
[M]^{-1}
\left[
\begin{array}{c}
F_1 \\
F_2
\end{array}
\right]
The solution can be determined easily numerically this way. Otherwise there is a lot of terms which lead to errors. This is what was done in the example below. The one major thing with the double pendulum problem is that it is one of the easiest systems that demonstrates chaotic behaviour, that is with small changes to any of the input parameters can produce rather different (and even unproducible) results.
Note, click here to view the above double pendulum example simulation in a separate tab.
Spring Pendulum
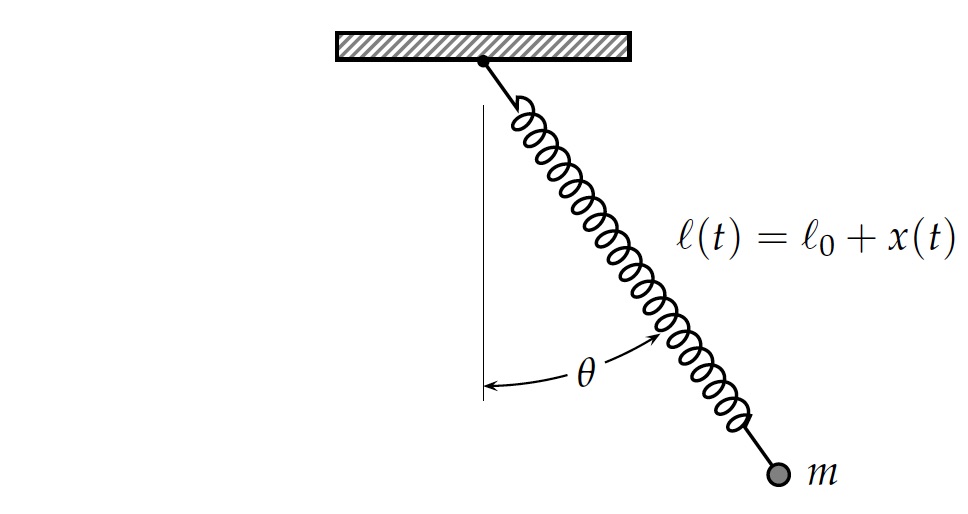
A spring pendulum is just like the simple pendulum but a spring is used instead of using a string. Note that we neglect the mass of the spring; we only care about the fact that can vary in length.
There are two degrees of freedom in this problem, which are the angle of the pendulum from the vertical (\theta) and the total length of the spring (\ell). The spring is assumed to have a force constant k and an equilibrium length \ell_0.
The position of the mass due to the motion of the pendulum and spring is:
x = \ell \sin \theta = (\ell_0 + x(t)) \sin \theta
\qquad
y = -\ell \cos \theta = -(\ell_0 + x(t)) \cos \theta
The velocity is a bit more complicated (remember to take both derivatives):
\dot{x} = (\ell_0 + x(t)) \cos \theta \cdot \dot{\theta} + \dot{x} \cdot \sin \theta
\qquad
\dot{y} = (\ell_0 + x(t)) \sin \theta \cdot \dot{\theta} – \dot{x} \cdot \cos \theta
\begin{aligned}
T = \frac{1}{2}mv^2 &= \frac{1}{2}m \left( v_\mathsf{spring}^2 + v_\mathsf{pend}^2 \right) \\
&= \frac{1}{2}m \left( \dot{x}^2 + \dot{y}^2 \right) \\
&= \frac{1}{2}m \left( ((\ell_0 + x(t)) \cos \theta \cdot \dot{\theta} + \dot{x} \cdot \sin \theta)^2 + ((\ell_0 + x(t)) \sin \theta\cdot\dot{\theta} – \dot{x} \cdot \cos \theta)^2 \right) \\
&= \frac{1}{2}m \left( (\ell_0 + x)^2 \cos^2 \theta \dot{\theta}^2 + 2(\ell_0 + x)\cos \theta\sin \theta \dot{\theta} \dot{x}+ \sin^2 \theta\dot{x}^2 \right) + \\
& \qquad\qquad\qquad \left( (\ell_0 + x)^2 \sin^2 \theta \dot{\theta}^2\ -\ 2(\ell_0 + x)\sin \theta\cos \theta \dot{\theta} \dot{x} + \cos^2 \theta \dot{x}^2 \right) \\
&= \frac{1}{2}m \left( (\ell_0 + x)^2 \dot{\theta}^2 + \dot{x}^2 \right) \\
\end{aligned}
\begin{aligned}
V = mgh + \frac{1}{2} kx^2
&= -mg\ell\cos\theta + \frac{1}{2} kx^2 \\
&= -mg(\ell_0 + x)\cos\theta + \frac{1}{2} kx^2
\end{aligned}
The Lagrangian now becomes:
\begin{aligned}
\mathcal{L} &= T – V \\
&= \frac{1}{2} m \dot{x}^2 + \frac{1}{2}m (\ell_0 + x)^2 \dot{\theta}^2 + mg(\ell_0 + x)\cos\theta\ -\ \frac{1}{2} kx^2
\end{aligned}
Since there are to degrees of freedom, then the Lagrangian will be solved for each of them.
\begin{aligned}
\frac{\partial \mathcal{L}}{\partial \dot{\theta}} &= m (\ell_0 + x)^2 \dot{\theta} \\
\frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{\theta}} \right) &= m (\ell_0 + x)^2 \ddot{\theta} + 2m (\ell_0 + x) \dot{\theta} \dot{x}\\
\frac{\partial \mathcal{L}}{\partial \theta} &= -mg(\ell_0 + x)\sin\theta \\
\frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{\theta}} \right)\ -\ \frac{\partial \mathcal{L}}{\partial \theta} &=
m (\ell_0 + x)^2 \ddot{\theta} + 2m (\ell_0 + x) \dot{\theta} \dot{x} + mg(\ell_0 + x)\sin\theta = 0 \\
&= (\ell_0 + x)^2 \ddot{\theta} + 2 (\ell_0 + x) \dot{\theta} \dot{x} + g(\ell_0 + x)\sin\theta = 0
\end{aligned}
\begin{aligned}
\frac{\partial \mathcal{L}}{\partial \dot{x}} &= m \dot{x} \\
\frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{x}} \right) &= m \ddot{x} \\
\frac{\partial \mathcal{L}}{\partial x} &= m (\ell_0 x) \dot{\theta}^2 + mg \cos \theta\ -\ kx \\
\frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{x}} \right)\ -\ \frac{\partial \mathcal{L}}{\partial x} &=
m \ddot{x}\ -\ m (\ell_0 + x) \dot{\theta}^2\ -\ mg \cos \theta + kx = 0 \\
&= \ddot{x}\ -\ (\ell_0 + x) \dot{\theta}^2\ -\ g \cos \theta + \frac{k}{m}x = 0
\end{aligned}
The final equations of motion are:
\begin{aligned}
\ddot{\theta} &= – \frac{2}{(\ell_0 + x)} \dot{\theta} \dot{x} – \frac{g}{(\ell_0 + x)} \sin\theta \\
\ddot{x} &= (\ell_0 + x) \dot{\theta}^2 + g \cos \theta – \frac{k}{m}x
\end{aligned}
Damping…
Some damping can be added to make things slightly more realistic in that things can eventually slow down and stop. However, to keep things simple a very easy to calculate form of damping was added, but it isn’t too accurate. So we have:
\frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{q}} \right)\ -\ \frac{\partial \mathcal{L}}{\partial q}
= \frac{\partial F}{\partial \dot{q}}
Again to keep things simple, the following is the damping:
F_{\dot{\theta}} = \frac{1}{2} b\dot{\theta}^2
\qquad\qquad
F_{\dot{x}} = \frac{1}{2} c \dot{x}^2
So for each simulation step we subtract the following from \ddot{\theta} and \ddot{x}:
\frac{\partial F}{\partial \dot{\theta}} = b\dot{\theta}
\qquad\qquad
\frac{\partial F}{\partial \dot{x}} = c\dot{x}
Finally, below is a small demonstration of a spring pendulum. Click here to view it on a separate tab.
Code
All the code of the pendulums (using javascript and the HTML canvas tag) along with a Latex document of all the math is available here.
DifferentialEquations Javascript Lagrangian Physics Simulation
No Comments