Every so often, I find doing some ‘recreation mathematics’ a weird type of fun. I know there are better things to spend my brain power on, so I try to limit such projects.
All of these projects are based on L-systems (or Lindenmayer systems) for a few reasons including: 1) they are fairly easy to implement; 2) it’s good to change one’s pace sometimes; and 3) can use the practice for some future projects (such as drawing plants).
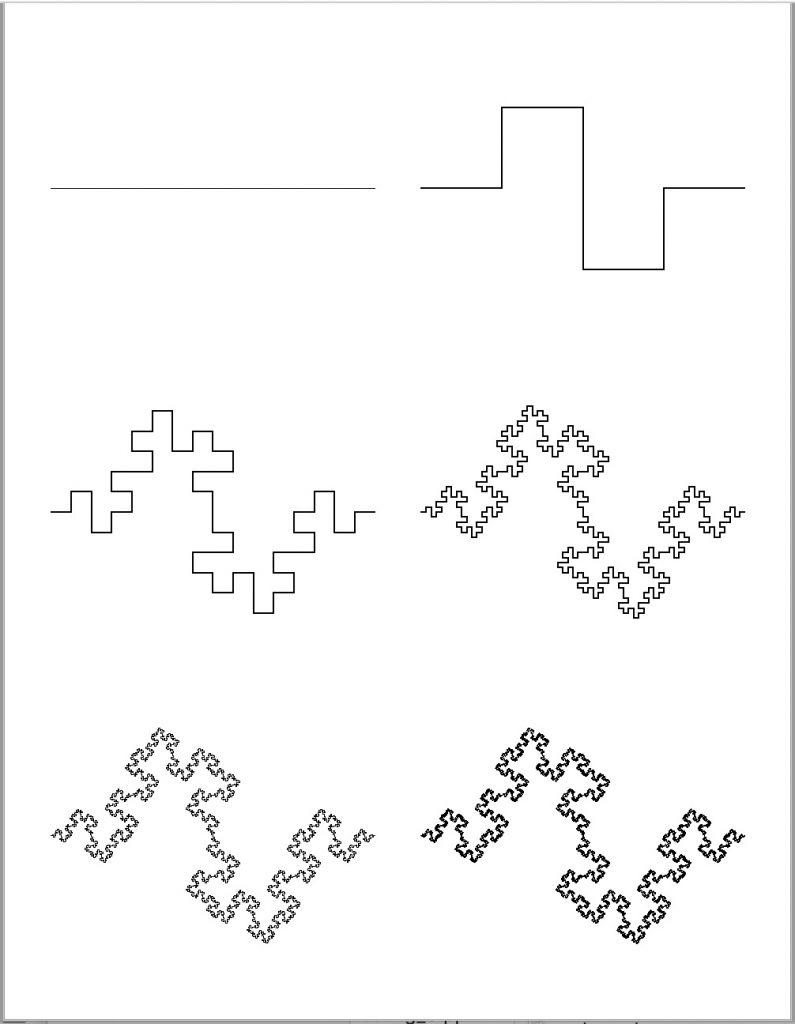
Cesàro curve fractals…
The Cesàro curve is a specific instance of the De Rham curve. It is similar to the Koch curve, however the angle is much tighter (usually 85o). The L-system can be described by:
Just a few iterations are needed to produce some interesting results. Below on the left is the Cesàro curve after 7 iterations. On the right is a series of 17 curves connected tip to tip where the angle increases by 5o (from 5o to 85o); this concept was inspired by Wolter Schraa’s range fractal.
Torn Square Fractal
By placing the Cesàro curve on the edges of a square, the torn square/paper fractal can be made. The big change required in the postscript code is with the axiom function as seen below:
/Axiom
{
RuleF
90 rotate RuleF
90 rotate RuleF
90 rotate RuleF
} defSince the curves form a closed shape, it can be filled in to make it appear as a torn piece of paper. Below on the left is the results after 7 iterations, while on the right is the first 5 iterations (the initial square is iteration zero).
Some Interesting Stuff…
A couple of interesting things that I have come across on the web…
- In this one math class (Math 207 at WWU), apparently this was part of a homework assignment once. In the homework solutions, there is a pretty cool animated gif.
- Its possible to get some cool t-shirts and notebooks with the Cesàro curve on it.
Code…
All the code that was used to make the above images is available here.
Minkowski sausage and islands…
The Minkowski curve is another very simple L-system based fractal. According to online sources, during the first few iterations the curve appears to resemble sausage links. The L-system to produce such a system is:
Note that there are a few slightly different versions of the main L-system rule out there (where some some rotations or flips exist); however they all produce similar looking results. Below on the left is Minkowski curve after 6 iterations, while in the image on the right contains iterations 0 to 5.
Minkowski island…
Similar to the torn square fractal, if the curve is placed on the edges of a square, then a closed in shape can be created which is referred to as the Minkowski island. Below on the left is the results after 5 iterations and on the right are iterations 0 to 3.
Applications…
One fairly interesting application where the Minkowski island fractal was used was described in this paper: Design of Miniaturized Frequency Selective Surfaces Using Minkowski Island Fractal. Another paper describes the usage in antenna design: Sausage Minkowski Square Patch Antenna for GPS Application.
Code…
The code to draw the above fractals is available here.
Dragon curves…
First the dragon curve (or curves since there are a few variations), can be a complete topic on its own. For now, we are limiting the scope to just one version of the curve produced by an l-system. There is a ton of information out there since its simple production rules can produce some rather complex designs. First some videos…
Vi Hart’s ‘Doodling in Math Class’ is a great video. Perhaps it should be mandatory watching for all kids stuck in boring math classes out there.
Numberphile has some great videos which I have linked to in the past. A lot of university lectures are pretty boring affairs, and their videos should be included as supplementary material.
Finally, a numberphile video with Donald Knuth talking about his dragon curve wall art piece that he and his wife made.
There are a few methods to create the dragon curve including: using an IFS, L-system, paper folding, and even copy and paste with a 90o rotation (as seen in above Vi Hart video). For the L-system, the basic rules are:
Note that there are some variations of the system which seem a little more complicated but often make things easier to draw since the start and end points from different iterations line up (after scaling of course). The following was adapted from L-Systems in Postscript, The Dragon Curve:
Then using this second system, the following was produced: on the left is the dragon curve after 17 iterations and on the right, iteration 0, 1, 2, 4, 8 and 12 are shown.
Rounded corners…
From the above images once can notice that curve seems to overlap with itself. This is not at all true, rather there are points when corners touch each other which make it appear that the curve overlaps. To fix this problem, the code changing the angle (that is the + and – rules), can be changed so that the angle is applied while also drawing a small step forward.
In the postscript code:
/alpha { 90 } def
/Minus { -1 alpha mul rotate } def
/Plus { alpha rotate } defbecomes…
/Step { 0.1 baselength mul 0.1 alpha mul cos div } def
/Minus { 10 { -0.1 alpha mul rotate Step 0 rlineto } repeat } def
/Plus { 10 { 0.1 alpha mul rotate Step 0 rlineto } repeat } defBelow are some images examples with the rounded corners. On the left is a dragon curve with 13 iteration with rounded corners, and on the right is a zoom in on one of the ‘islands’ that was drawn on a blue background to make it that much more fun.
Some items of interest…
The dragon curve is perhaps one of the more popular fractal objects out there and can be found in a variety of places including:
Code…
The code for the above fractals is available here.











No Comments