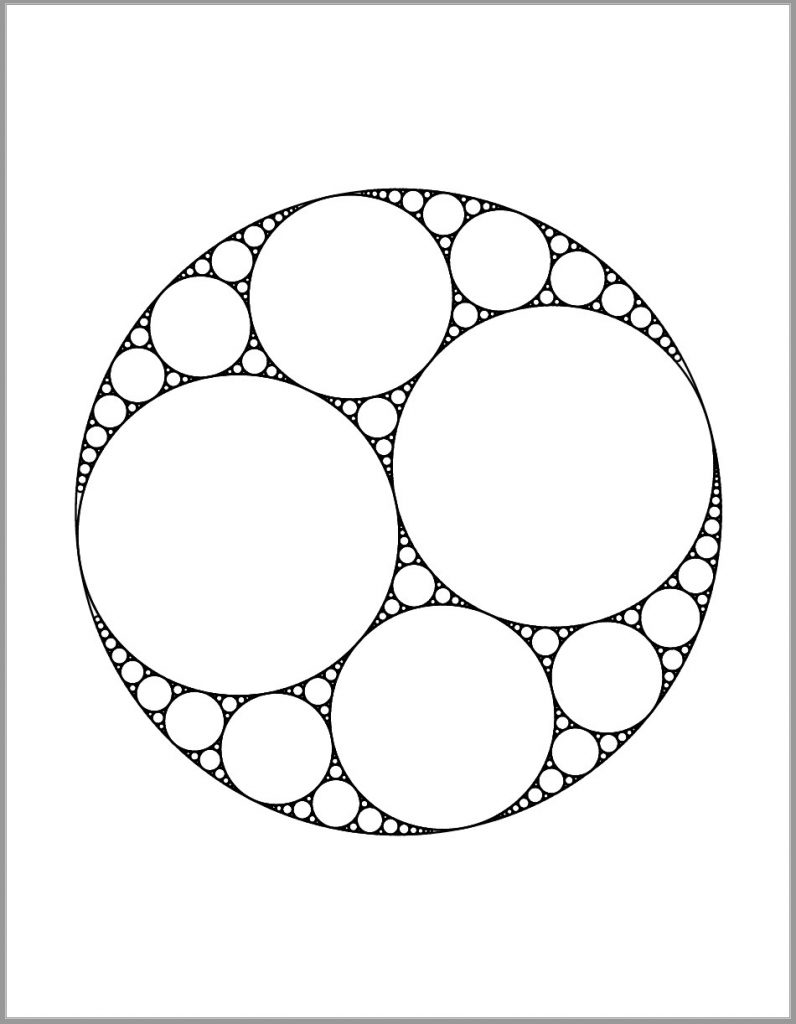
To continue on with the other fractals in postscript I have chosen to work on the Apollonian Gasket. It consists of a set of circles where a circle is tangent to three other circles.
Descartes Theorem
Starting with three tangent circles, two other tangent circles can be calculated using Descartes’ theorem, that is:
Where b_1, b_2, b_3 are the ‘bends’ of the known three circles and b_4 is the bend of the unknown circle to be solved for. The bends are similar to the curvature but also consider the ‘direction’ of the circle. Mathematically the bend and curvature is defined as:
The ‘direction’ is defined as:
Therefore the bend is:
Descartes Theorem can easily be solved to give the following solution:
Therefore, by recursively applying Descartes Theorem we can produce an Apollonian gasket, however we still need to determine where the centres of the new circles are in order to draw them.
The Complex Descartes Theorem
The complex Descartes theorem doesn’t appear to be that much of a big step from the standard Descartes Theorem, however without it would very difficult to compute an Apollonian gasket. I believe that is was first introduced in the following paper (there is some heavy math in the proof):
The main change to the theorem is to include in the circle centres written as complex numbers (noted as z_i) as follows:
Note that a slightly more elegant way to write this is:
Then given 3 circles with known radius and centre, the final radius and centre can be computed using the equation above for b_4 and the following:
Being slightly more simple
To generate the solution, we need to recursively solve the above equations by using different combinations of the original circles with the generated values. Because of the plus/minus in the above equations, with recursion it can be rather inefficient since its possible to produce pre-existing solutions repeatedly. Therefore it is slightly easier to compute the + version of b_4 and sparingly use the – version. Note that it can be easily be computed by (note that this is the same for both the complex solution as well):
Implementation
The code was written in python that output the results to postscript. There were a few reasons for this: 1) in raw postscript some additional code would have been necessary to deal with any math related to deal with complex values while this is readily available in python (in the cmath package); 2) since postscript files can be easily converted to PDFs, it is very easy to generate vector graphics this way.
In the implementation, initially one large circle (of radius 3.5 inches) is placed in the centre of the output page and two smaller circles are placed tangent to each other. It is possible to control the radii of the smaller circles to obtain a variety of different solutions.
One other option allows the user to generate results purely using lines or filling the circles with various colours.
Note that the code is available in the following GitHub repository (in the ApollonianGasket*.py files).
Results
Two example solutions are shown below. The output in the left most image is circle edge version (with line thickness of 1.5pts), while the output in the right has the circles filled with colours that are normally distributed about a dark blue shade (hex code #336699)
Other Solutions
The Apollonian gasket is a known problem and I have looked at purely for general interest and some form of entertainment. There are plenty of other interesting cases/versions/solutions out on the internet including:
- Implementations written in Haskell, Lisp, and Javascript
- This pretty great article
- Some interesting tattoos… like this one
- An interactive web-based version

No Comments